
Question Number 206443 by Safojon last updated on 14/Apr/24

Commented by necx122 last updated on 15/Apr/24
getting a more detailed solution will be excellent for us. I still tried going through the solution already done but I couldn't understand the approaches readily. Please, whoever can expound would be a help. Thanks.
Commented by A5T last updated on 15/Apr/24
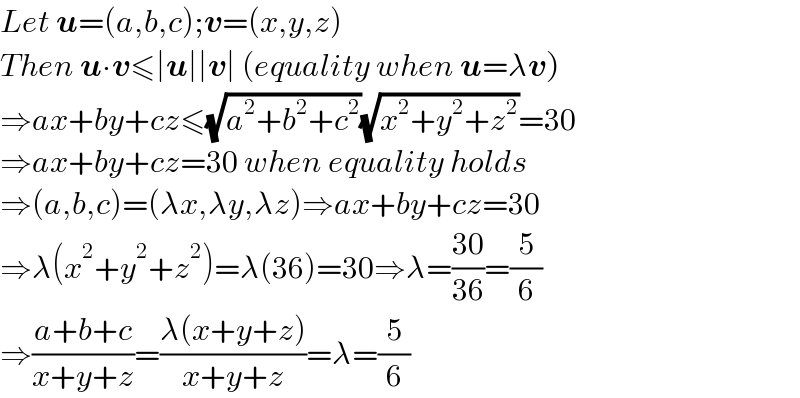
$${Let}\:\boldsymbol{{u}}=\left({a},{b},{c}\right);\boldsymbol{{v}}=\left({x},{y},{z}\right) \\ $$$${Then}\:\boldsymbol{{u}}\centerdot\boldsymbol{{v}}\leqslant\mid\boldsymbol{{u}}\mid\mid\boldsymbol{{v}}\mid\:\left({equality}\:{when}\:\boldsymbol{{u}}=\lambda\boldsymbol{{v}}\right) \\ $$$$\Rightarrow{ax}+{by}+{cz}\leqslant\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }=\mathrm{30} \\ $$$$\Rightarrow{ax}+{by}+{cz}=\mathrm{30}\:{when}\:{equality}\:{holds} \\ $$$$\Rightarrow\left({a},{b},{c}\right)=\left(\lambda{x},\lambda{y},\lambda{z}\right)\Rightarrow{ax}+{by}+{cz}=\mathrm{30} \\ $$$$\Rightarrow\lambda\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)=\lambda\left(\mathrm{36}\right)=\mathrm{30}\Rightarrow\lambda=\frac{\mathrm{30}}{\mathrm{36}}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\Rightarrow\frac{{a}+{b}+{c}}{{x}+{y}+{z}}=\frac{\lambda\left({x}+{y}+{z}\right)}{{x}+{y}+{z}}=\lambda=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Commented by MATHEMATICSAM last updated on 14/Apr/24

$$\mathrm{Q}\:\mathrm{193296} \\ $$
Commented by necx122 last updated on 16/Apr/24
Wow!!! I've been able to solve along and understand. Thanks to everyone that attempted this problem.
