Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 206442 by universe last updated on 14/Apr/24

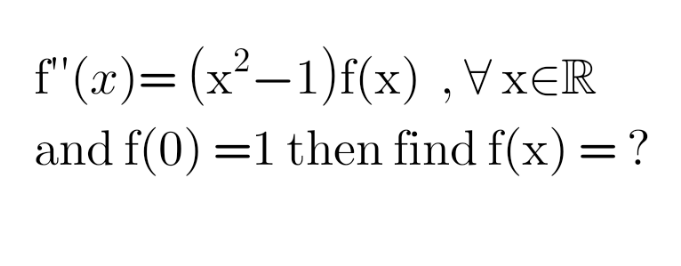
Answered by Berbere last updated on 14/Apr/24

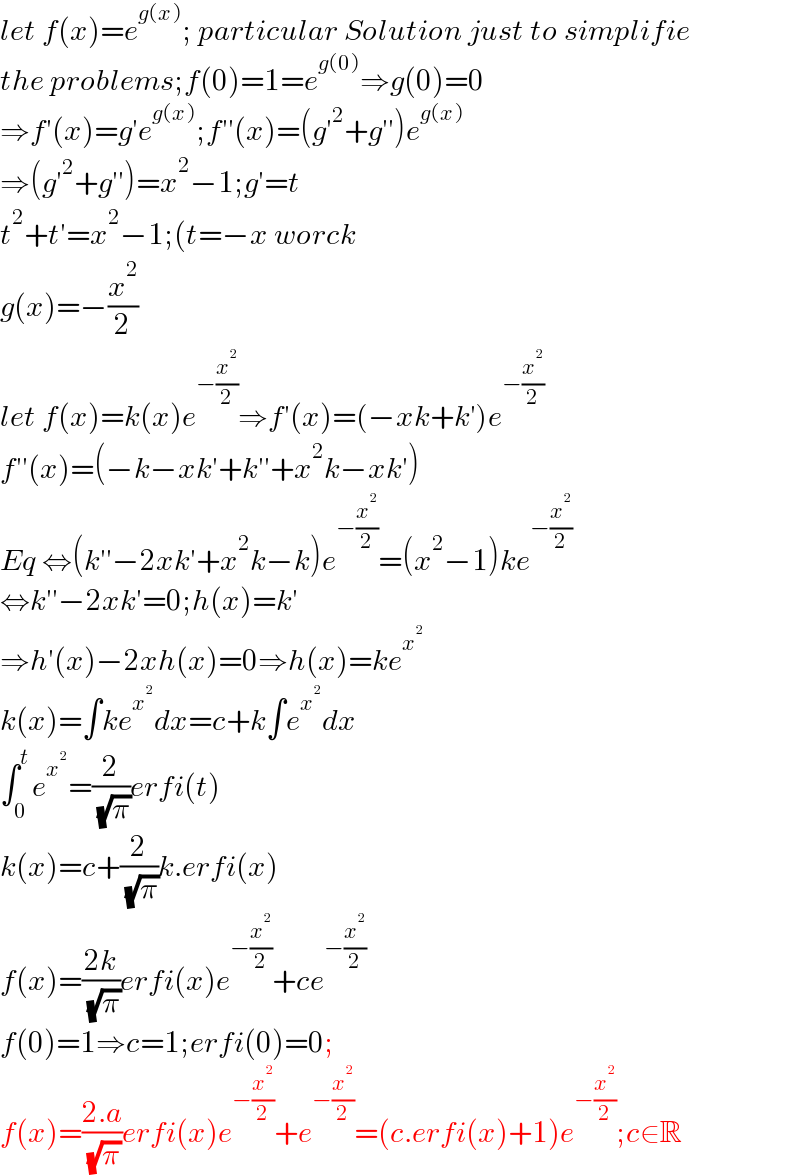
let f(x)=e^(g(x)) ; particular Solution just to simplifie the problems;f(0)=1=e^(g(0)) ⇒g(0)=0 ⇒f′(x)=g′e^(g(x)) ;f′′(x)=(g′^2 +g′′)e^(g(x)) ⇒(g′^2 +g′′)=x^2 −1;g′=t t^2 +t′=x^2 −1;(t=−x worck g(x)=−(x^2 /2) let f(x)=k(x)e^(−(x^2 /2)) ⇒f′(x)=(−xk+k′)e^(−(x^2 /2)) f′′(x)=(−k−xk′+k′′+x^2 k−xk′) Eq ⇔(k′′−2xk′+x^2 k−k)e^(−(x^2 /2)) =(x^2 −1)ke^(−(x^2 /2)) ⇔k′′−2xk′=0;h(x)=k′ ⇒h′(x)−2xh(x)=0⇒h(x)=ke^x^2 k(x)=∫ke^x^2 dx=c+k∫e^x^2 dx ∫_0 ^t e^x^2 =(2/( (√π)))erfi(t) k(x)=c+(2/( (√π)))k.erfi(x) f(x)=((2k)/( (√π)))erfi(x)e^(−(x^2 /2)) +ce^(−(x^2 /2)) f(0)=1⇒c=1;erfi(0)=0; f(x)=((2.a)/( (√π)))erfi(x)e^(−(x^2 /2)) +e^(−(x^2 /2)) =(c.erfi(x)+1)e^(−(x^2 /2)) ;c∈R

$${let}\:{f}\left({x}\right)={e}^{{g}\left({x}\right)} ;\:{particular}\:{Solution}\:{just}\:{to}\:{simplifie} \\ $$$${the}\:{problems};{f}\left(\mathrm{0}\right)=\mathrm{1}={e}^{{g}\left(\mathrm{0}\right)} \Rightarrow{g}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}'\left({x}\right)={g}'{e}^{{g}\left({x}\right)} ;{f}''\left({x}\right)=\left({g}'^{\mathrm{2}} +{g}''\right){e}^{{g}\left({x}\right)} \\ $$$$\Rightarrow\left({g}'^{\mathrm{2}} +{g}''\right)={x}^{\mathrm{2}} −\mathrm{1};{g}'={t} \\ $$$${t}^{\mathrm{2}} +{t}'={x}^{\mathrm{2}} −\mathrm{1};\left({t}=−{x}\:{worck}\right. \\ $$$${g}\left({x}\right)=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\: \\ $$$${let}\:{f}\left({x}\right)={k}\left({x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \Rightarrow{f}'\left({x}\right)=\left(−{xk}+{k}'\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${f}''\left({x}\right)=\left(−{k}−{xk}'+{k}''+{x}^{\mathrm{2}} {k}−{xk}'\right) \\ $$$${Eq}\:\Leftrightarrow\left({k}''−\mathrm{2}{xk}'+{x}^{\mathrm{2}} {k}−{k}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} =\left({x}^{\mathrm{2}} −\mathrm{1}\right){ke}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\Leftrightarrow{k}''−\mathrm{2}{xk}'=\mathrm{0};{h}\left({x}\right)={k}' \\ $$$$\Rightarrow{h}'\left({x}\right)−\mathrm{2}{xh}\left({x}\right)=\mathrm{0}\Rightarrow{h}\left({x}\right)={ke}^{{x}^{\mathrm{2}} } \\ $$$${k}\left({x}\right)=\int{ke}^{{x}^{\mathrm{2}} } {dx}={c}+{k}\int{e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$\int_{\mathrm{0}} ^{{t}} {e}^{{x}^{\mathrm{2}} } =\frac{\mathrm{2}}{\:\sqrt{\pi}}{erfi}\left({t}\right) \\ $$$${k}\left({x}\right)={c}+\frac{\mathrm{2}}{\:\sqrt{\pi}}{k}.{erfi}\left({x}\right) \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{k}}{\:\sqrt{\pi}}{erfi}\left({x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +{ce}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1}\Rightarrow{c}=\mathrm{1};{erfi}\left(\mathrm{0}\right)=\mathrm{0}; \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}.{a}}{\:\sqrt{\pi}}{erfi}\left({x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} =\left({c}.{erfi}\left({x}\right)+\mathrm{1}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} ;{c}\in\mathbb{R} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com