Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 206399 by BaliramKumar last updated on 13/Apr/24

Commented by mr W last updated on 14/Apr/24

since the question asks the ratio of “their” speeds, answers (b), (c), (d) are all correct. when the question asks the ratio of the speeds of “dog, lion and fox”, then only answer (c) is correct.

$${since}\:{the}\:{question}\:{asks}\:{the}\:{ratio}\:{of} \\ $$$$``{their}''\:{speeds},\:{answers}\:\left({b}\right),\:\left({c}\right),\:\left({d}\right) \\ $$$${are}\:{all}\:{correct}. \\ $$$${when}\:{the}\:{question}\:{asks}\:{the}\:{ratio}\:{of} \\ $$$${the}\:{speeds}\:{of}\:``{dog},\:{lion}\:{and}\:{fox}'',\: \\ $$$${then}\:{only}\:{answer}\:\left({c}\right)\:{is}\:{correct}. \\ $$

Answered by mr W last updated on 13/Apr/24

distance covered by each jump from dog, lion and fox is: J_D , J_L , J_F speed of dog, lion and fox: v_D , v_L , v_F 8J_D =16J_L =24J_F ⇒J_D =2J_L =3J_F t=((8J_D )/v_D )=((12J_L )/v_L )=((15J_F )/v_F ) ⇒((8J_D )/v_D )=((6J_D )/v_L )=((5J_D )/v_F ) ⇒(8/v_D )=(6/v_L )=(5/v_F ) ⇒v_D :v_L :v_F =8:6:5 ⇒answer (C)

$${distance}\:{covered}\:{by}\:{each}\:{jump}\:{from} \\ $$$${dog},\:{lion}\:{and}\:{fox}\:{is}:\:{J}_{{D}} ,\:{J}_{{L}} ,\:{J}_{{F}} \\ $$$${speed}\:{of}\:{dog},\:{lion}\:{and}\:{fox}:\:{v}_{{D}} ,\:{v}_{{L}} ,\:{v}_{{F}} \\ $$$$ \\ $$$$\mathrm{8}{J}_{{D}} =\mathrm{16}{J}_{{L}} =\mathrm{24}{J}_{{F}} \\ $$$$\Rightarrow{J}_{{D}} =\mathrm{2}{J}_{{L}} =\mathrm{3}{J}_{{F}} \\ $$$${t}=\frac{\mathrm{8}{J}_{{D}} }{{v}_{{D}} }=\frac{\mathrm{12}{J}_{{L}} }{{v}_{{L}} }=\frac{\mathrm{15}{J}_{{F}} }{{v}_{{F}} } \\ $$$$\Rightarrow\frac{\mathrm{8}{J}_{{D}} }{{v}_{{D}} }=\frac{\mathrm{6}{J}_{{D}} }{{v}_{{L}} }=\frac{\mathrm{5}{J}_{{D}} }{{v}_{{F}} }\:\Rightarrow\frac{\mathrm{8}}{{v}_{{D}} }=\frac{\mathrm{6}}{{v}_{{L}} }=\frac{\mathrm{5}}{{v}_{{F}} }\: \\ $$$$\Rightarrow{v}_{{D}} :{v}_{{L}} :{v}_{{F}} =\mathrm{8}:\mathrm{6}:\mathrm{5} \\ $$$$\Rightarrow{answer}\:\left({C}\right) \\ $$

Commented by BaliramKumar last updated on 13/Apr/24

thanks

$$\mathrm{thanks} \\ $$

Answered by A5T last updated on 13/Apr/24

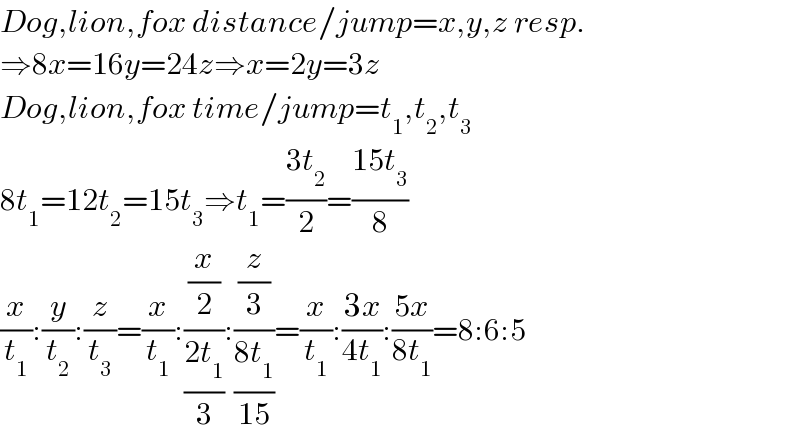
Dog,lion,fox distance/jump=x,y,z resp. ⇒8x=16y=24z⇒x=2y=3z Dog,lion,fox time/jump=t_1 ,t_2 ,t_3 8t_1 =12t_2 =15t_3 ⇒t_1 =((3t_2 )/2)=((15t_3 )/8) (x/t_1 ):(y/t_2 ):(z/t_3 )=(x/t_1 ):((x/2)/((2t_1 )/3)):((z/3)/((8t_1 )/(15)))=(x/t_1 ):((3x)/(4t_1 )):((5x)/(8t_1 ))=8:6:5

$${Dog},{lion},{fox}\:{distance}/{jump}={x},{y},{z}\:{resp}. \\ $$$$\Rightarrow\mathrm{8}{x}=\mathrm{16}{y}=\mathrm{24}{z}\Rightarrow{x}=\mathrm{2}{y}=\mathrm{3}{z} \\ $$$${Dog},{lion},{fox}\:{time}/{jump}={t}_{\mathrm{1}} ,{t}_{\mathrm{2}} ,{t}_{\mathrm{3}} \\ $$$$\mathrm{8}{t}_{\mathrm{1}} =\mathrm{12}{t}_{\mathrm{2}} =\mathrm{15}{t}_{\mathrm{3}} \Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{3}{t}_{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{15}{t}_{\mathrm{3}} }{\mathrm{8}} \\ $$$$\frac{{x}}{{t}_{\mathrm{1}} }:\frac{{y}}{{t}_{\mathrm{2}} }:\frac{{z}}{{t}_{\mathrm{3}} }=\frac{{x}}{{t}_{\mathrm{1}} }:\frac{\frac{{x}}{\mathrm{2}}}{\frac{\mathrm{2}{t}_{\mathrm{1}} }{\mathrm{3}}}:\frac{\frac{{z}}{\mathrm{3}}}{\frac{\mathrm{8}{t}_{\mathrm{1}} }{\mathrm{15}}}=\frac{{x}}{{t}_{\mathrm{1}} }:\frac{\mathrm{3}{x}}{\mathrm{4}{t}_{\mathrm{1}} }:\frac{\mathrm{5}{x}}{\mathrm{8}{t}_{\mathrm{1}} }=\mathrm{8}:\mathrm{6}:\mathrm{5} \\ $$

Commented by BaliramKumar last updated on 13/Apr/24

thanks

$$\mathrm{thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com