
Question Number 206364 by Skabetix last updated on 12/Apr/24
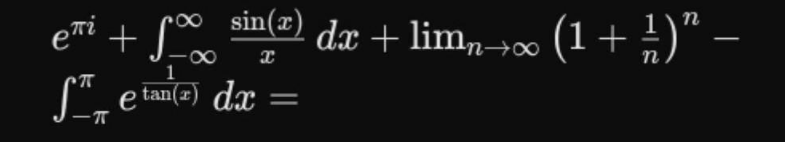
Answered by TonyCWX08 last updated on 13/Apr/24
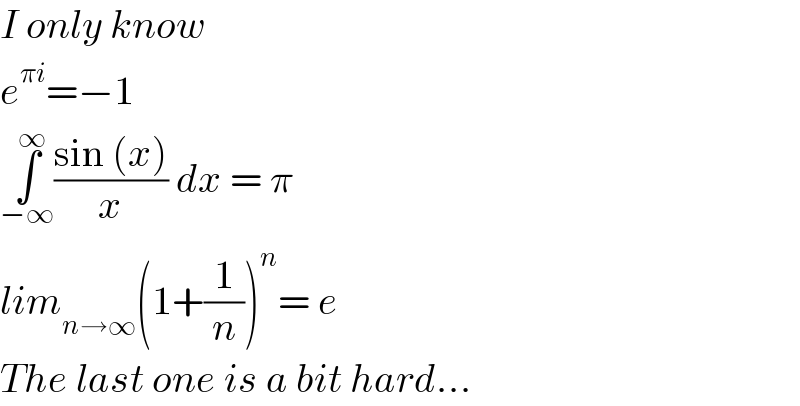
$${I}\:{only}\:{know} \\ $$$${e}^{\pi{i}} =−\mathrm{1} \\ $$$$\underset{−\infty} {\overset{\infty} {\int}}\frac{\mathrm{sin}\:\left({x}\right)}{{x}}\:{dx}\:=\:\pi \\ $$$${lim}_{{n}\rightarrow\infty} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} =\:{e} \\ $$$${The}\:{last}\:{one}\:{is}\:{a}\:{bit}\:{hard}... \\ $$
Answered by Berbere last updated on 13/Apr/24
![∫_(−π) ^π e^(1/(tan(x))) dx≥∫_0 ^(π/2) e^(1/(tan(x))) dx=∫_0 ^∞ e^(1/y) (dy/(1+y^2 ))=∫_0 ^∞ (y^2 /(1+y^2 ))e^y dy >∫_0 ^∞ (y^2 /(1+y^2 ))dy=[y−tan^(−1) (y)]_0 ^∞ =∞ diverge](Q206389.png)
$$\int_{−\pi} ^{\pi} {e}^{\frac{\mathrm{1}}{{tan}\left({x}\right)}} {dx}\geqslant\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{\frac{\mathrm{1}}{{tan}\left({x}\right)}} {dx}=\int_{\mathrm{0}} ^{\infty} {e}^{\frac{\mathrm{1}}{{y}}} \frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\infty} \frac{{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }{e}^{{y}} {dy} \\ $$$$>\int_{\mathrm{0}} ^{\infty} \frac{{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }{dy}=\left[{y}−\mathrm{tan}^{−\mathrm{1}} \left({y}\right)\right]_{\mathrm{0}} ^{\infty} =\infty\:{diverge} \\ $$
