Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 206157 by cortano21 last updated on 08/Apr/24

Commented by cortano21 last updated on 08/Apr/24

$$\:\:\:\:\:\cancel{\underline{\underbrace{ }}} \\ $$

Commented by A5T last updated on 09/Apr/24

This is generally not uniquely defined. One can come up with mathematically correct solutions with different answers. Points A such that ((AB)/(AP))=(5/3) lie on the Apollonius circle.

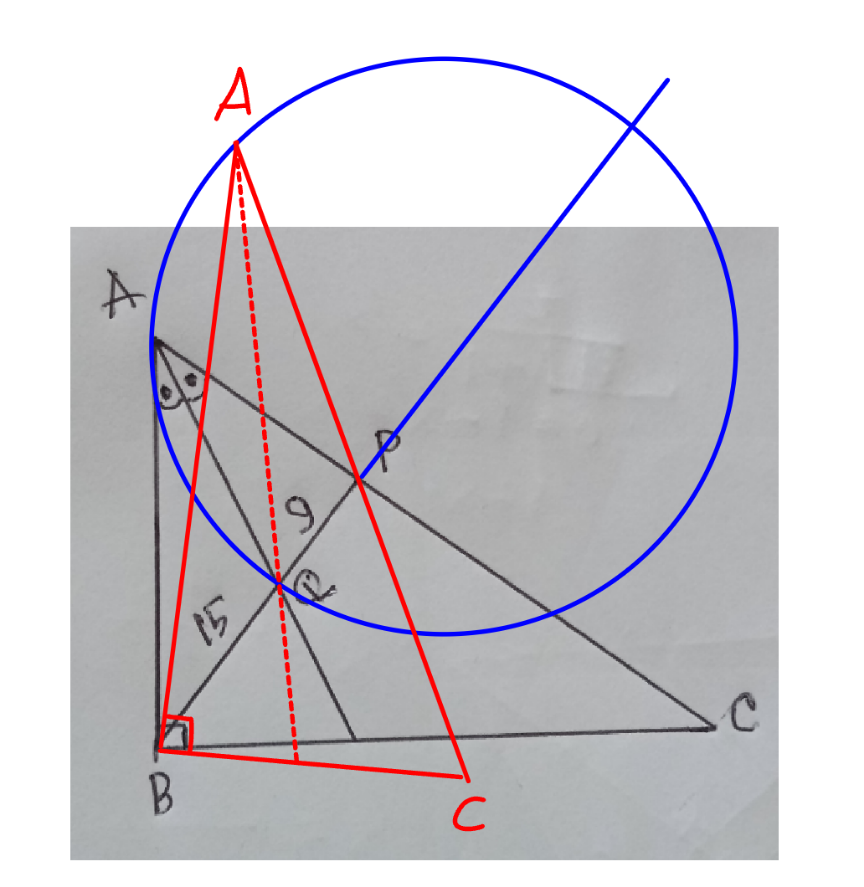
$${This}\:{is}\:{generally}\:{not}\:{uniquely}\:{defined}.\:{One}\:{can} \\ $$$${come}\:{up}\:{with}\:{mathematically}\:{correct}\:{solutions} \\ $$$${with}\:{different}\:{answers}.\:{Points}\:{A}\:{such}\:{that}\: \\ $$$$\frac{{AB}}{{AP}}=\frac{\mathrm{5}}{\mathrm{3}}\:{lie}\:{on}\:{the}\:{Apollonius}\:{circle}. \\ $$

Commented by A5T last updated on 09/Apr/24

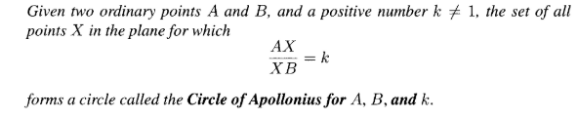
Answered by dimentri last updated on 08/Apr/24

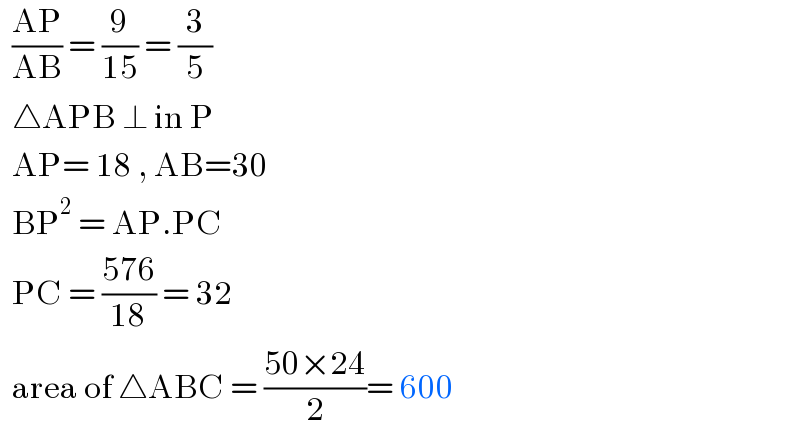
((AP)/(AB)) = (9/(15)) = (3/5) △APB ⊥ in P AP= 18 , AB=30 BP^2 = AP.PC PC = ((576)/(18)) = 32 area of △ABC = ((50×24)/2)= 600

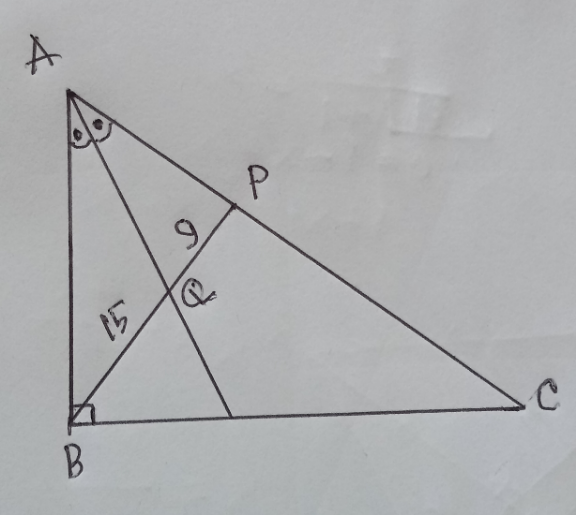
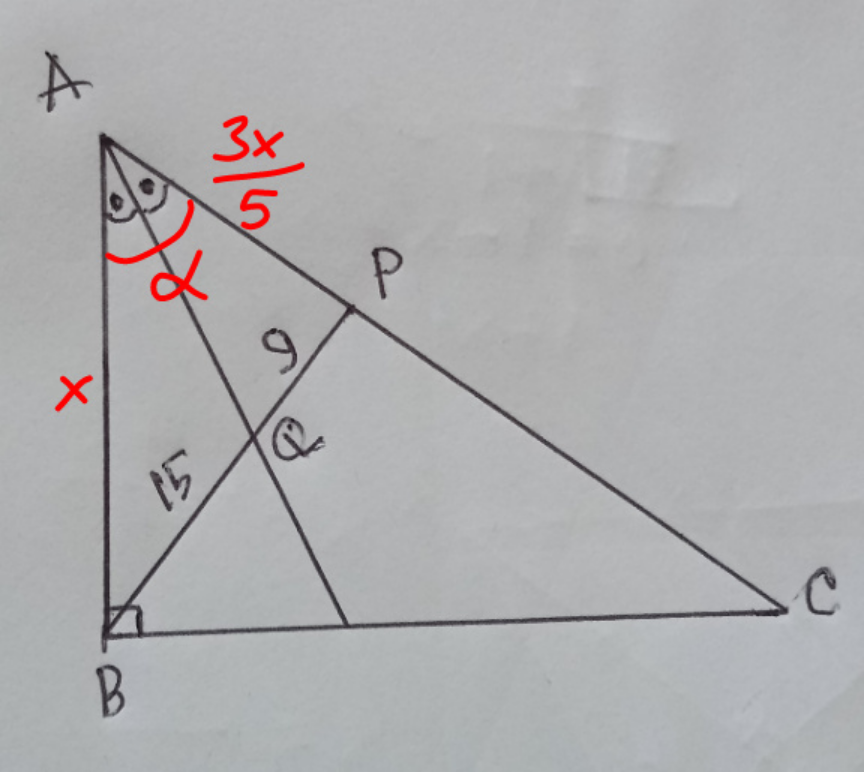
$$\:\:\frac{\mathrm{AP}}{\mathrm{AB}}\:=\:\frac{\mathrm{9}}{\mathrm{15}}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\:\:\bigtriangleup\mathrm{APB}\:\bot\:\mathrm{in}\:\mathrm{P} \\ $$$$\:\:\mathrm{AP}=\:\mathrm{18}\:,\:\mathrm{AB}=\mathrm{30} \\ $$$$\:\:\mathrm{BP}^{\mathrm{2}} \:=\:\mathrm{AP}.\mathrm{PC}\: \\ $$$$\:\:\mathrm{PC}\:=\:\frac{\mathrm{576}}{\mathrm{18}}\:=\:\mathrm{32} \\ $$$$\:\:\mathrm{area}\:\mathrm{of}\:\bigtriangleup\mathrm{ABC}\:=\:\frac{\mathrm{50}×\mathrm{24}}{\mathrm{2}}=\:\mathrm{600} \\ $$

Commented by mr W last updated on 08/Apr/24

i think it is not said that AP⊥BC.

$${i}\:{think}\:{it}\:{is}\:{not}\:{said}\:{that}\:{AP}\bot{BC}. \\ $$

Answered by mr W last updated on 08/Apr/24

Commented by mr W last updated on 09/Apr/24

say AB=x ((AP)/9)=(x/(15)) ⇒AP=((3x)/5) (15+9)^2 =x^2 +(((3x)/5))^2 −2x×((3x)/5) cos α ⇒x^2 =((7200)/(17−15 cos α)) area of ΔABC: Δ=((x^2 tan α)/2)=((3600 tan α)/(17−15 cos α)) we see the triangle ABC is not unique and its area is also not unique. for locus of point A see also Q181759

$${say}\:{AB}={x} \\ $$$$\frac{{AP}}{\mathrm{9}}=\frac{{x}}{\mathrm{15}}\:\Rightarrow{AP}=\frac{\mathrm{3}{x}}{\mathrm{5}} \\ $$$$\left(\mathrm{15}+\mathrm{9}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\left(\frac{\mathrm{3}{x}}{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{2}{x}×\frac{\mathrm{3}{x}}{\mathrm{5}}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{\mathrm{7200}}{\mathrm{17}−\mathrm{15}\:\mathrm{cos}\:\alpha} \\ $$$${area}\:{of}\:\Delta{ABC}: \\ $$$$\Delta=\frac{{x}^{\mathrm{2}} \:\mathrm{tan}\:\alpha}{\mathrm{2}}=\frac{\mathrm{3600}\:\mathrm{tan}\:\alpha}{\mathrm{17}−\mathrm{15}\:\mathrm{cos}\:\alpha} \\ $$$${we}\:{see}\:{the}\:{triangle}\:{ABC}\:{is}\:{not} \\ $$$${unique}\:{and}\:{its}\:{area}\:{is}\:{also}\:{not} \\ $$$${unique}. \\ $$$${for}\:{locus}\:{of}\:{point}\:{A}\:{see}\:{also} \\ $$$${Q}\mathrm{181759} \\ $$

Commented by mr W last updated on 08/Apr/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com