Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 206003 by mnjuly1970 last updated on 04/Apr/24

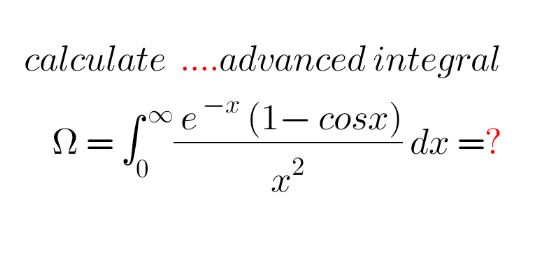
Answered by Berbere last updated on 04/Apr/24

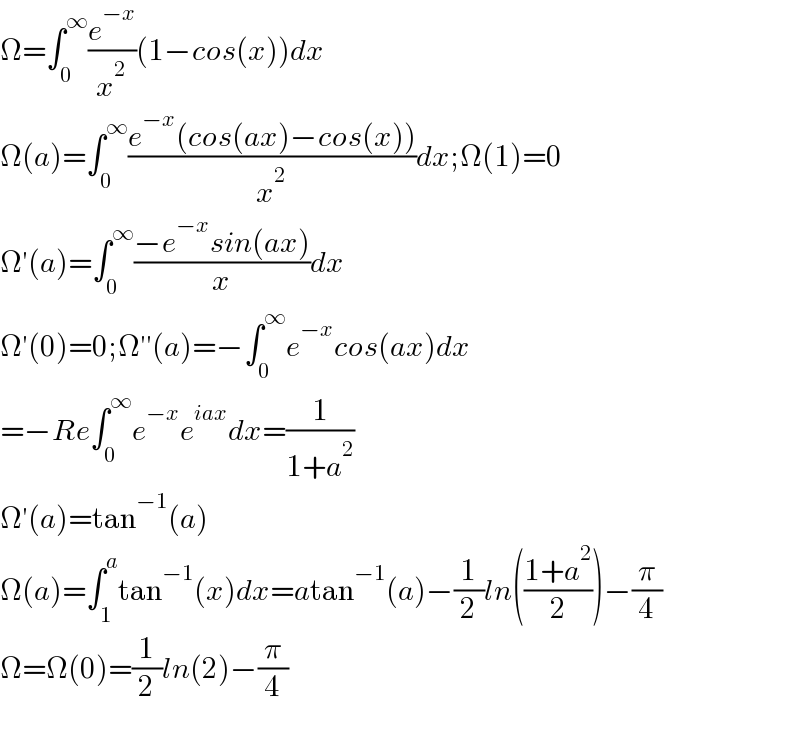
Ω=∫_0 ^∞ (e^(−x) /x^2 )(1−cos(x))dx Ω(a)=∫_0 ^∞ ((e^(−x) (cos(ax)−cos(x)))/x^2 )dx;Ω(1)=0 Ω′(a)=∫_0 ^∞ ((−e^(−x) sin(ax))/x)dx Ω′(0)=0;Ω′′(a)=−∫_0 ^∞ e^(−x) cos(ax)dx =−Re∫_0 ^∞ e^(−x) e^(iax) dx=(1/(1+a^2 )) Ω′(a)=tan^(−1) (a) Ω(a)=∫_1 ^a tan^(−1) (x)dx=atan^(−1) (a)−(1/2)ln(((1+a^2 )/2))−(π/4) Ω=Ω(0)=(1/2)ln(2)−(π/4)

$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} }{{x}^{\mathrm{2}} }\left(\mathrm{1}−{cos}\left({x}\right)\right){dx} \\ $$$$\Omega\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} \left({cos}\left({ax}\right)−{cos}\left({x}\right)\right)}{{x}^{\mathrm{2}} }{dx};\Omega\left(\mathrm{1}\right)=\mathrm{0} \\ $$$$\Omega'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{−{e}^{−{x}} {sin}\left({ax}\right)}{{x}}{dx} \\ $$$$\Omega'\left(\mathrm{0}\right)=\mathrm{0};\Omega''\left({a}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {cos}\left({ax}\right){dx} \\ $$$$=−{Re}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {e}^{{iax}} {dx}=\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$$\Omega'\left({a}\right)=\mathrm{tan}^{−\mathrm{1}} \left({a}\right) \\ $$$$\Omega\left({a}\right)=\int_{\mathrm{1}} ^{{a}} \mathrm{tan}^{−\mathrm{1}} \left({x}\right){dx}={a}\mathrm{tan}^{−\mathrm{1}} \left({a}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{a}^{\mathrm{2}} }{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$$\Omega=\Omega\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$

Answered by mathzup last updated on 05/Apr/24

I=_(by parts) [−(1/x)e^(−x) (1−cosx)]_0 ^(+∞) −∫_0 ^∞ (−(1/x)){−e^(−x) (1−cosx)+e^(−x) sinx}dx =0+∫_0 ^∞ (1/x)(e^(−x) (sinx+cosx−1))dx =∫_0 ^∞ (e^(−x) /x)(sinx+cosx−1)dx f(λ)=∫_0 ^∞ (e^(−λx) /x)(sinx+cosx−1)dx f^′ (λ)=−∫_0 ^∞ e^(−λx) (sinx+cosx−1)dx =∫_0 ^∞ e^(−λx) dx−∫_0 ^∞ e^(−λx) (cosx+sinx)dx but ∫_0 ^∞ e^(−λx) dx=[−(1/λ)e^(−λx) ]_0 ^∞ =(1/λ) ∫_0 ^∞ e^(−λx) (cosx +sinx)dx =Re(∫_0 ^∞ e^(−λx+ix) dx)+Im(∫_0 ^∞ e^(−λx+ix) dx) ∫_0 ^∞ e^((−λ+i)x) dx=[(1/(−λ+i))e^((−λ+i)x) ]_0 ^∞ =−(1/(−λ+i))=(1/(λ−i))=((λ+i)/(1+λ^2 )) ⇒ R(...)=(λ/(1+λ^2 )) and Im(...)=(1/(1+λ^2 )) ⇒f^′ (λ)=(1/λ)−(λ/(1+λ^2 ))−(1/(1+λ^2 )) ⇒ f(λ)=ln(λ)−(1/2)ln(λ^2 +1)−arctanλ +c lim_(λ→+∞) =0=−(π/2)+c ⇒c=(π/2) ⇒f(λ)=ln((λ/( (√(1+λ^2 )))))−arctanλ +(π/2) I=f(1)=ln((1/( (√2))))−(π/4)+(π/2) =−(1/2)ln(2)+(π/4) ⇒ I=(π/4)−(1/2)ln(2)

$${I}=_{{by}\:{parts}} \left[−\frac{\mathrm{1}}{{x}}{e}^{−{x}} \left(\mathrm{1}−{cosx}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$−\int_{\mathrm{0}} ^{\infty} \:\left(−\frac{\mathrm{1}}{{x}}\right)\left\{−{e}^{−{x}} \left(\mathrm{1}−{cosx}\right)+{e}^{−{x}} {sinx}\right\}{dx} \\ $$$$=\mathrm{0}+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{x}}\left({e}^{−{x}} \left({sinx}+{cosx}−\mathrm{1}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} }{{x}}\left({sinx}+{cosx}−\mathrm{1}\right){dx} \\ $$$${f}\left(\lambda\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\lambda{x}} }{{x}}\left({sinx}+{cosx}−\mathrm{1}\right){dx} \\ $$$${f}^{'} \left(\lambda\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−\lambda{x}} \left({sinx}+{cosx}−\mathrm{1}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\lambda{x}} {dx}−\int_{\mathrm{0}} ^{\infty} \:{e}^{−\lambda{x}} \left({cosx}+{sinx}\right){dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\lambda{x}} {dx}=\left[−\frac{\mathrm{1}}{\lambda}{e}^{−\lambda{x}} \right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\lambda} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−\lambda{x}} \left({cosx}\:+{sinx}\right){dx} \\ $$$$={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−\lambda{x}+{ix}} {dx}\right)+{Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\lambda{x}+{ix}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−\lambda+{i}\right){x}} {dx}=\left[\frac{\mathrm{1}}{−\lambda+{i}}{e}^{\left(−\lambda+{i}\right){x}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{−\lambda+{i}}=\frac{\mathrm{1}}{\lambda−{i}}=\frac{\lambda+{i}}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${R}\left(...\right)=\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }\:{and}\:{Im}\left(...\right)=\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow{f}^{'} \left(\lambda\right)=\frac{\mathrm{1}}{\lambda}−\frac{\lambda}{\mathrm{1}+\lambda^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}\left(\lambda\right)={ln}\left(\lambda\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\lambda^{\mathrm{2}} +\mathrm{1}\right)−{arctan}\lambda\:+{c} \\ $$$${lim}_{\lambda\rightarrow+\infty} =\mathrm{0}=−\frac{\pi}{\mathrm{2}}+{c}\:\Rightarrow{c}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{f}\left(\lambda\right)={ln}\left(\frac{\lambda}{\:\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }}\right)−{arctan}\lambda\:+\frac{\pi}{\mathrm{2}} \\ $$$${I}={f}\left(\mathrm{1}\right)={ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$${I}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com