
Question Number 205880 by cortano12 last updated on 01/Apr/24
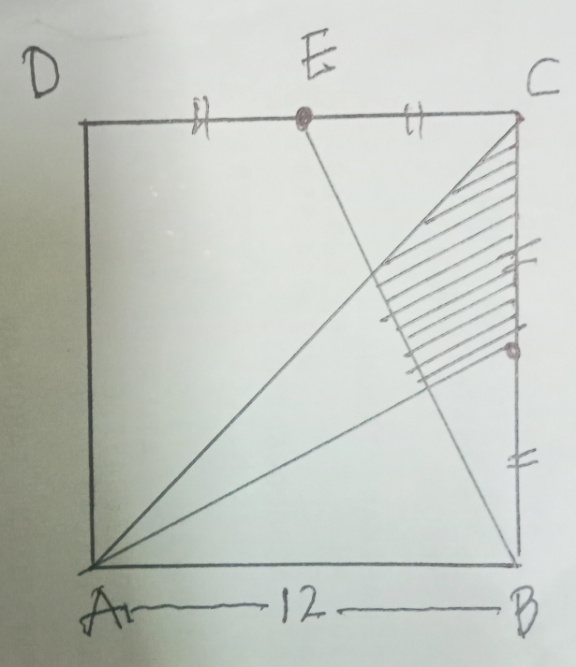
Commented by cortano12 last updated on 01/Apr/24

$$ \\ $$
Answered by mr W last updated on 02/Apr/24
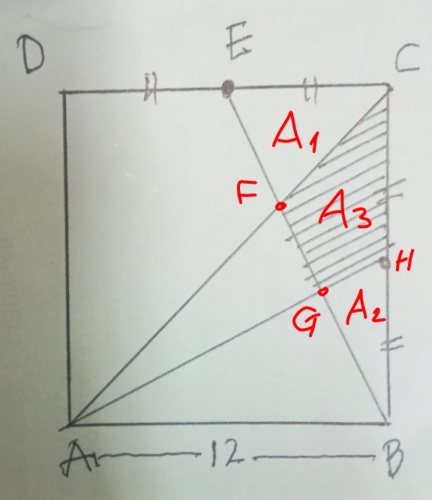
Commented by mr W last updated on 02/Apr/24
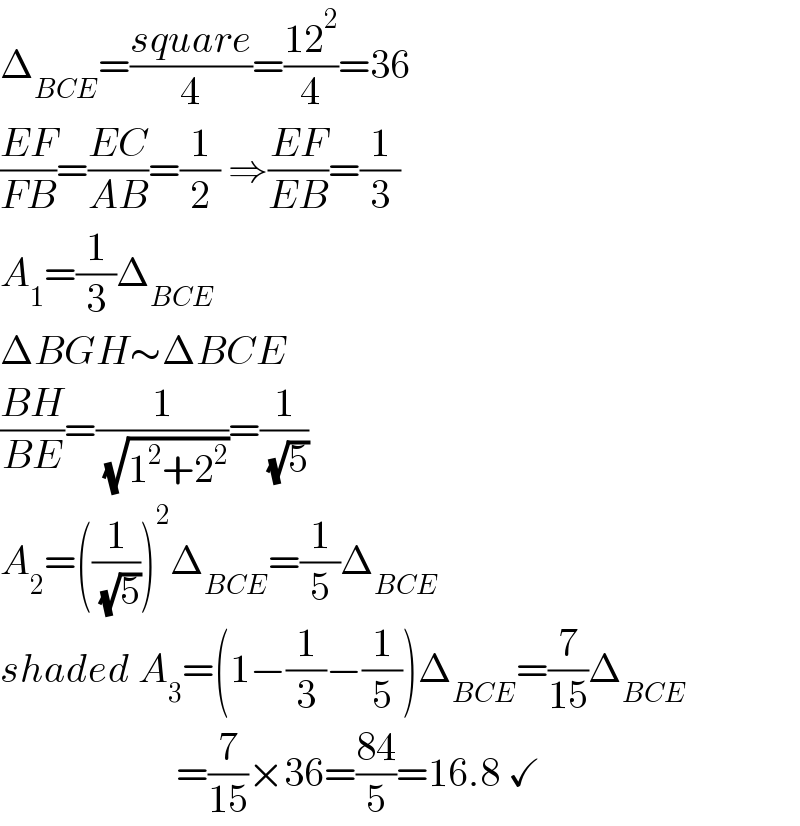
$$\Delta_{{BCE}} =\frac{{square}}{\mathrm{4}}=\frac{\mathrm{12}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{36} \\ $$$$\frac{{EF}}{{FB}}=\frac{{EC}}{{AB}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\frac{{EF}}{{EB}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\Delta_{{BCE}} \\ $$$$\Delta{BGH}\sim\Delta{BCE} \\ $$$$\frac{{BH}}{{BE}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${A}_{\mathrm{2}} =\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \Delta_{{BCE}} =\frac{\mathrm{1}}{\mathrm{5}}\Delta_{{BCE}} \\ $$$${shaded}\:{A}_{\mathrm{3}} =\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}\right)\Delta_{{BCE}} =\frac{\mathrm{7}}{\mathrm{15}}\Delta_{{BCE}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{7}}{\mathrm{15}}×\mathrm{36}=\frac{\mathrm{84}}{\mathrm{5}}=\mathrm{16}.\mathrm{8}\:\checkmark \\ $$
Answered by A5T last updated on 01/Apr/24
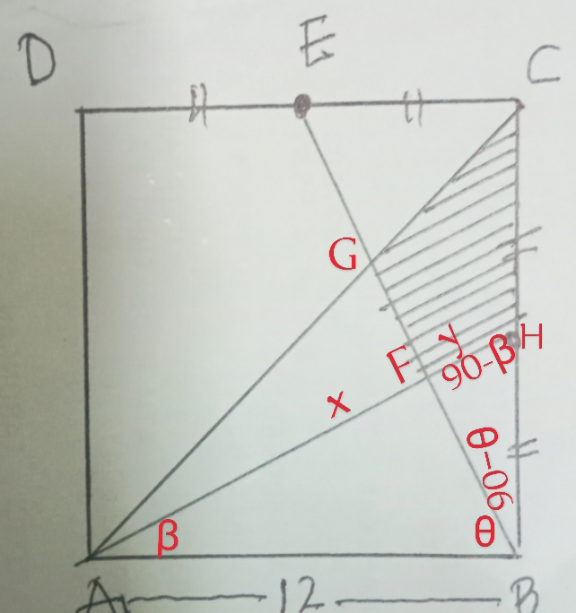
Commented by A5T last updated on 01/Apr/24
![((sin(90−θ))/(y=FH))=((sin(90−β))/(BF)); ((sinβ)/(BF))=((sinθ)/x) x=((BFsinθ)/(sinβ));(1/y)=((sin(90−β))/(BFsin(90−θ)))⇒(x/y)=((tanθ)/(tanβ))=((2/1)/(1/2))=4 (((1/2)×4y×2z)/((1/2)×5y×3z))=(8/(15))=(([AGF])/([ACH]))⇒(8/(15))×36=[AGF]=19.2 ⇒[CGFH]=[ACH]−[AGF]=36−19.2=16.8](Q205890.png)
$$\frac{{sin}\left(\mathrm{90}−\theta\right)}{{y}={FH}}=\frac{{sin}\left(\mathrm{90}−\beta\right)}{{BF}};\:\frac{{sin}\beta}{{BF}}=\frac{{sin}\theta}{{x}} \\ $$$${x}=\frac{{BFsin}\theta}{{sin}\beta};\frac{\mathrm{1}}{{y}}=\frac{{sin}\left(\mathrm{90}−\beta\right)}{{BFsin}\left(\mathrm{90}−\theta\right)}\Rightarrow\frac{{x}}{{y}}=\frac{{tan}\theta}{{tan}\beta}=\frac{\frac{\mathrm{2}}{\mathrm{1}}}{\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{4} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}{y}×\mathrm{2}{z}}{\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{5}{y}×\mathrm{3}{z}}=\frac{\mathrm{8}}{\mathrm{15}}=\frac{\left[{AGF}\right]}{\left[{ACH}\right]}\Rightarrow\frac{\mathrm{8}}{\mathrm{15}}×\mathrm{36}=\left[{AGF}\right]=\mathrm{19}.\mathrm{2} \\ $$$$\Rightarrow\left[{CGFH}\right]=\left[{ACH}\right]−\left[{AGF}\right]=\mathrm{36}−\mathrm{19}.\mathrm{2}=\mathrm{16}.\mathrm{8} \\ $$
