
Question Number 205861 by mr W last updated on 01/Apr/24
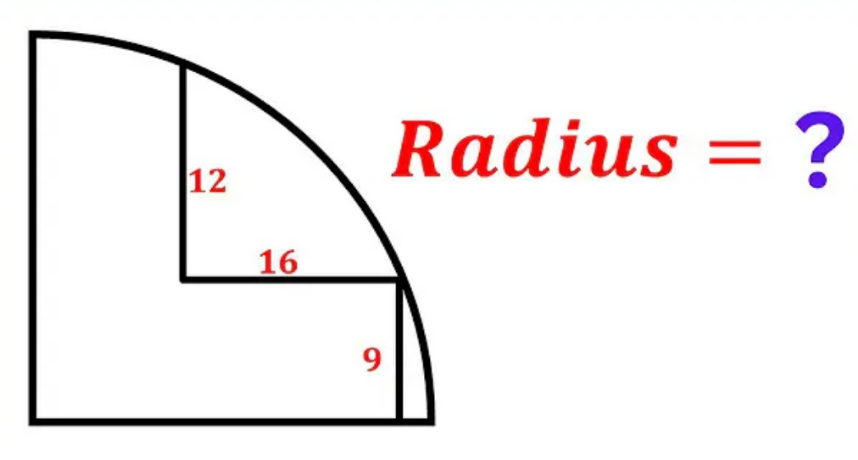
Answered by A5T last updated on 01/Apr/24
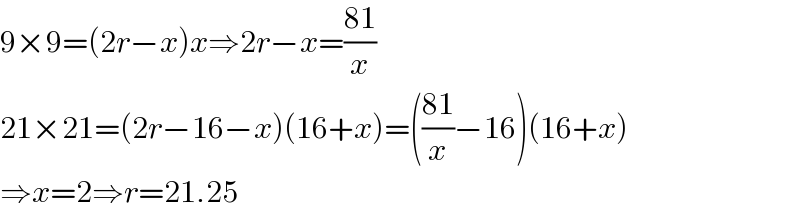
$$\mathrm{9}×\mathrm{9}=\left(\mathrm{2}{r}−{x}\right){x}\Rightarrow\mathrm{2}{r}−{x}=\frac{\mathrm{81}}{{x}} \\ $$$$\mathrm{21}×\mathrm{21}=\left(\mathrm{2}{r}−\mathrm{16}−{x}\right)\left(\mathrm{16}+{x}\right)=\left(\frac{\mathrm{81}}{{x}}−\mathrm{16}\right)\left(\mathrm{16}+{x}\right) \\ $$$$\Rightarrow{x}=\mathrm{2}\Rightarrow{r}=\mathrm{21}.\mathrm{25} \\ $$
Commented by mr W last updated on 01/Apr/24
��
Answered by mr W last updated on 01/Apr/24
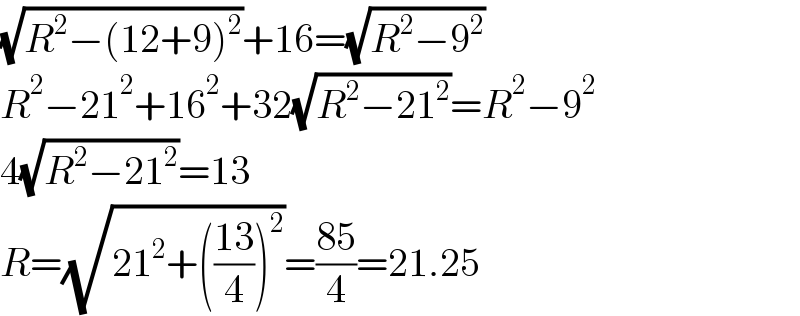
$$\sqrt{{R}^{\mathrm{2}} −\left(\mathrm{12}+\mathrm{9}\right)^{\mathrm{2}} }+\mathrm{16}=\sqrt{{R}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} −\mathrm{21}^{\mathrm{2}} +\mathrm{16}^{\mathrm{2}} +\mathrm{32}\sqrt{{R}^{\mathrm{2}} −\mathrm{21}^{\mathrm{2}} }={R}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \\ $$$$\mathrm{4}\sqrt{{R}^{\mathrm{2}} −\mathrm{21}^{\mathrm{2}} }=\mathrm{13} \\ $$$${R}=\sqrt{\mathrm{21}^{\mathrm{2}} +\left(\frac{\mathrm{13}}{\mathrm{4}}\right)^{\mathrm{2}} }=\frac{\mathrm{85}}{\mathrm{4}}=\mathrm{21}.\mathrm{25} \\ $$
Commented by Skabetix last updated on 02/Apr/24

$$ \\ $$Hello sir, how did you arrive at the first equation? Which theorems did you use? Congratulations anyway.
Commented by mr W last updated on 02/Apr/24
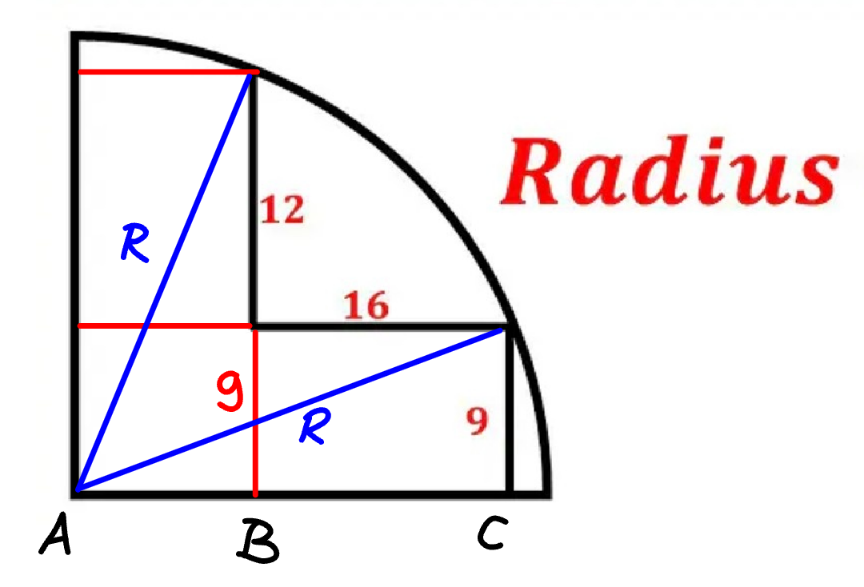
Commented by mr W last updated on 02/Apr/24
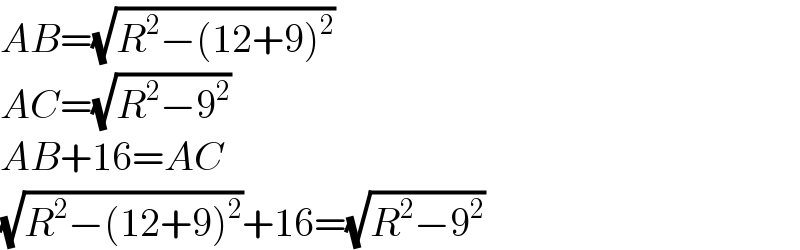
$${AB}=\sqrt{{R}^{\mathrm{2}} −\left(\mathrm{12}+\mathrm{9}\right)^{\mathrm{2}} } \\ $$$${AC}=\sqrt{{R}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} } \\ $$$${AB}+\mathrm{16}={AC} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\left(\mathrm{12}+\mathrm{9}\right)^{\mathrm{2}} }+\mathrm{16}=\sqrt{{R}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} } \\ $$
Answered by mr W last updated on 01/Apr/24
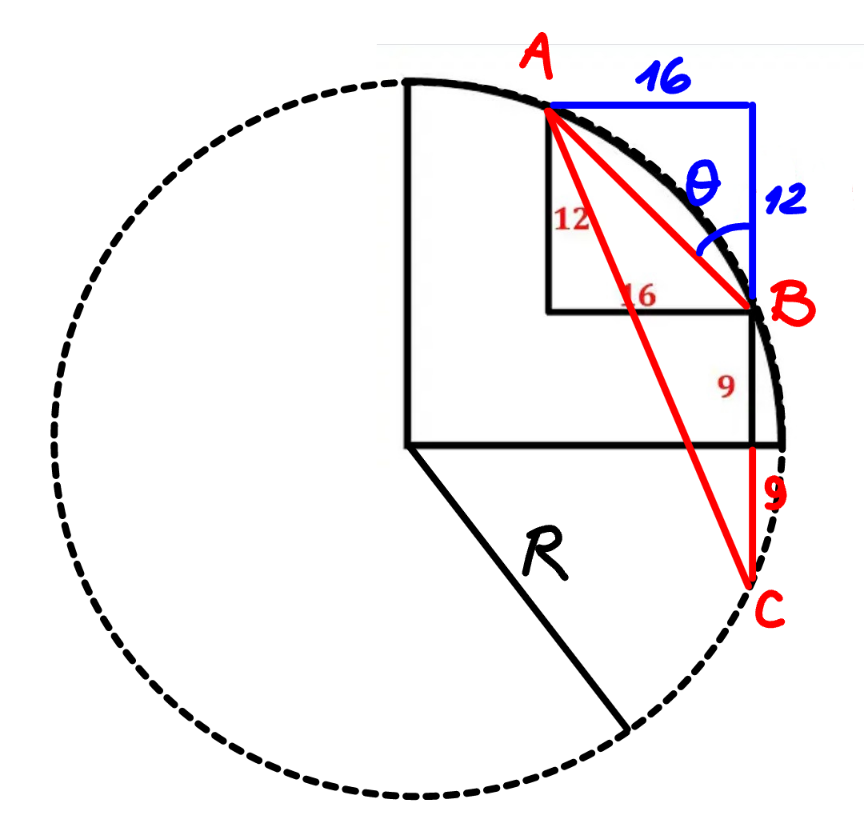
Commented by mr W last updated on 01/Apr/24
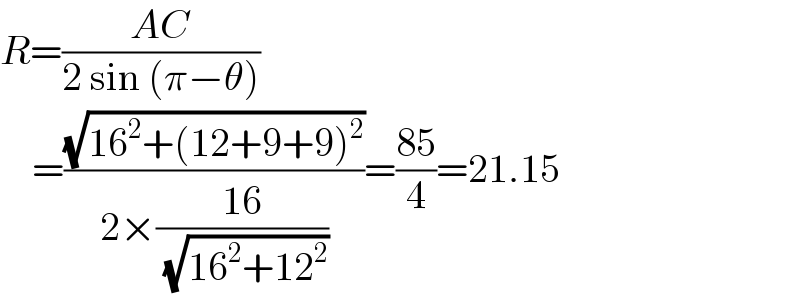
$${R}=\frac{{AC}}{\mathrm{2}\:\mathrm{sin}\:\left(\pi−\theta\right)} \\ $$$$\:\:\:\:=\frac{\sqrt{\mathrm{16}^{\mathrm{2}} +\left(\mathrm{12}+\mathrm{9}+\mathrm{9}\right)^{\mathrm{2}} }}{\mathrm{2}×\frac{\mathrm{16}}{\:\sqrt{\mathrm{16}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }}}=\frac{\mathrm{85}}{\mathrm{4}}=\mathrm{21}.\mathrm{15} \\ $$
