Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 205535 by cortano12 last updated on 24/Mar/24

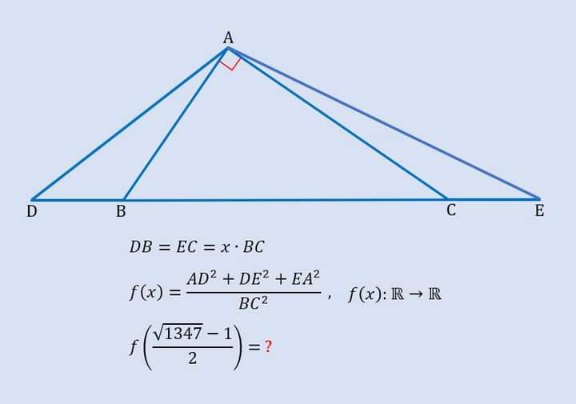
Answered by A5T last updated on 24/Mar/24

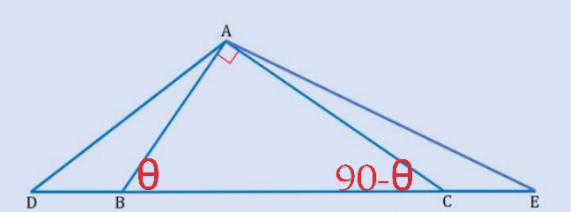
Commented by A5T last updated on 24/Mar/24

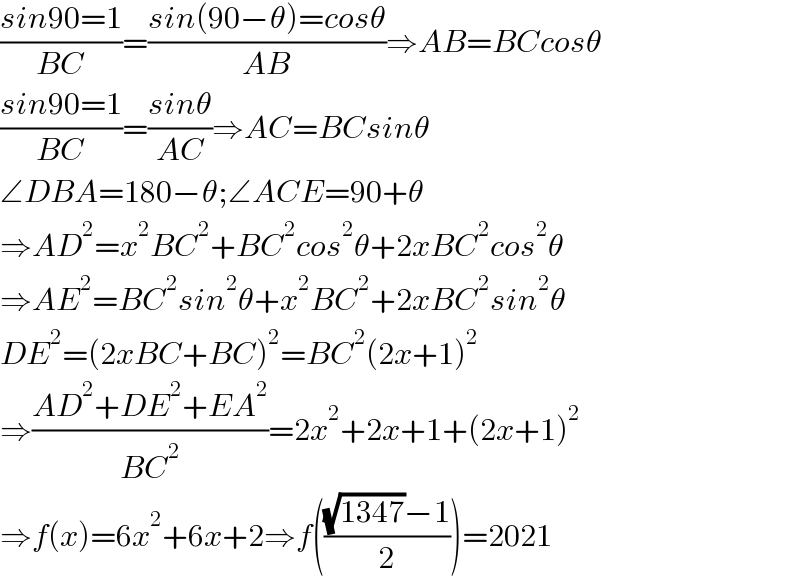
((sin90=1)/(BC))=((sin(90−θ)=cosθ)/(AB))⇒AB=BCcosθ ((sin90=1)/(BC))=((sinθ)/(AC))⇒AC=BCsinθ ∠DBA=180−θ;∠ACE=90+θ ⇒AD^2 =x^2 BC^2 +BC^2 cos^2 θ+2xBC^2 cos^2 θ ⇒AE^2 =BC^2 sin^2 θ+x^2 BC^2 +2xBC^2 sin^2 θ DE^2 =(2xBC+BC)^2 =BC^2 (2x+1)^2 ⇒((AD^2 +DE^2 +EA^2 )/(BC^2 ))=2x^2 +2x+1+(2x+1)^2 ⇒f(x)=6x^2 +6x+2⇒f((((√(1347))−1)/2))=2021

$$\frac{{sin}\mathrm{90}=\mathrm{1}}{{BC}}=\frac{{sin}\left(\mathrm{90}−\theta\right)={cos}\theta}{{AB}}\Rightarrow{AB}={BCcos}\theta \\ $$$$\frac{{sin}\mathrm{90}=\mathrm{1}}{{BC}}=\frac{{sin}\theta}{{AC}}\Rightarrow{AC}={BCsin}\theta \\ $$$$\angle{DBA}=\mathrm{180}−\theta;\angle{ACE}=\mathrm{90}+\theta \\ $$$$\Rightarrow{AD}^{\mathrm{2}} ={x}^{\mathrm{2}} {BC}^{\mathrm{2}} +{BC}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta+\mathrm{2}{xBC}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta \\ $$$$\Rightarrow{AE}^{\mathrm{2}} ={BC}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{x}^{\mathrm{2}} {BC}^{\mathrm{2}} +\mathrm{2}{xBC}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta \\ $$$${DE}^{\mathrm{2}} =\left(\mathrm{2}{xBC}+{BC}\right)^{\mathrm{2}} ={BC}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{AD}^{\mathrm{2}} +{DE}^{\mathrm{2}} +{EA}^{\mathrm{2}} }{{BC}^{\mathrm{2}} }=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}+\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}\Rightarrow{f}\left(\frac{\sqrt{\mathrm{1347}}−\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2021} \\ $$

Answered by mr W last updated on 24/Mar/24

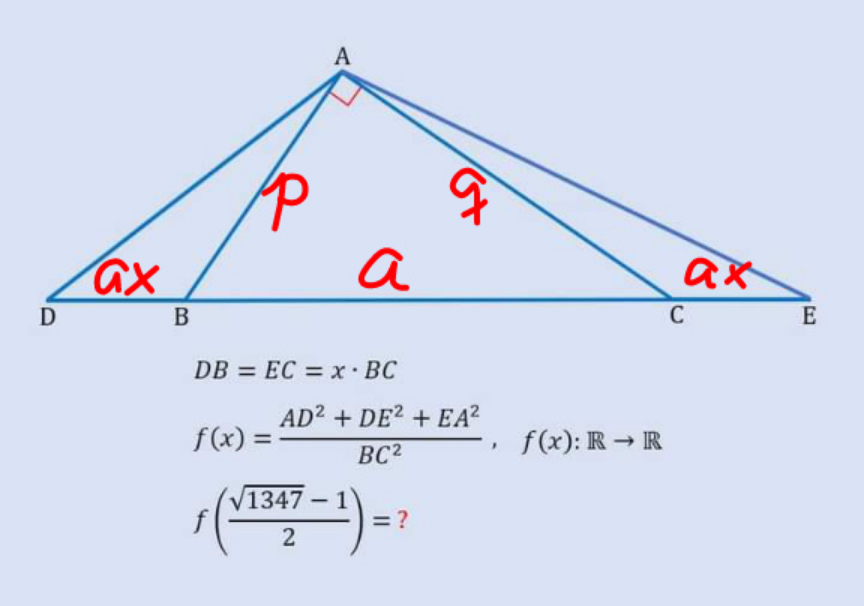
Commented by mr W last updated on 24/Mar/24

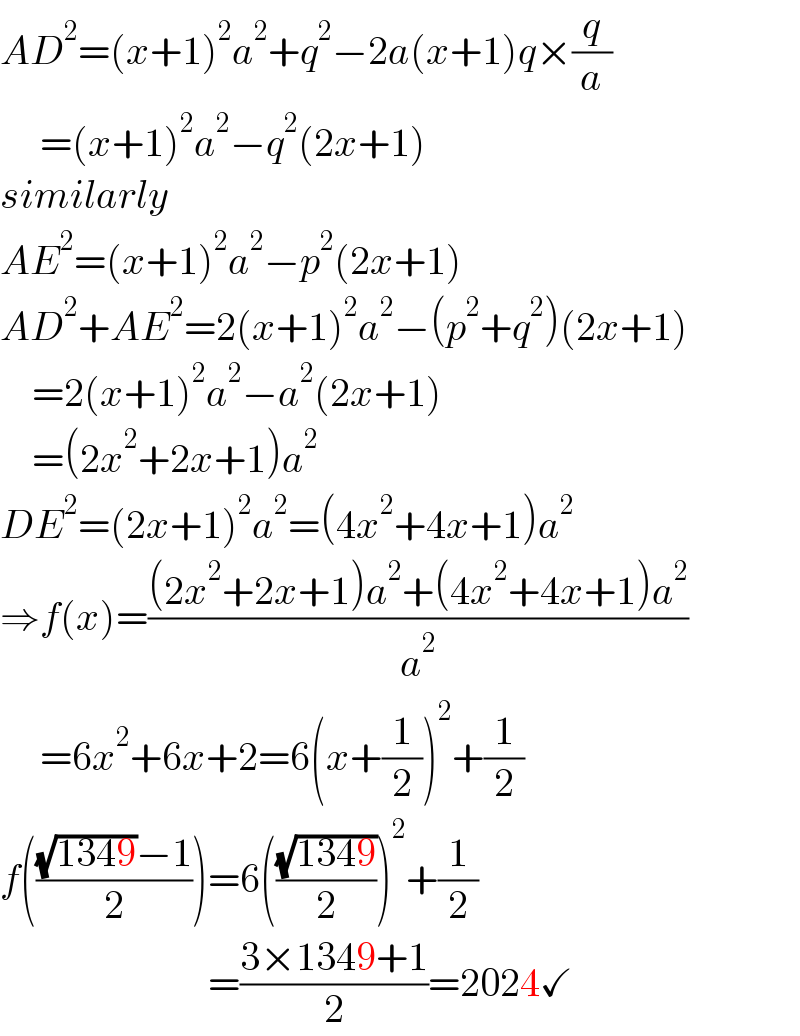
AD^2 =(x+1)^2 a^2 +q^2 −2a(x+1)q×(q/a) =(x+1)^2 a^2 −q^2 (2x+1) similarly AE^2 =(x+1)^2 a^2 −p^2 (2x+1) AD^2 +AE^2 =2(x+1)^2 a^2 −(p^2 +q^2 )(2x+1) =2(x+1)^2 a^2 −a^2 (2x+1) =(2x^2 +2x+1)a^2 DE^2 =(2x+1)^2 a^2 =(4x^2 +4x+1)a^2 ⇒f(x)=(((2x^2 +2x+1)a^2 +(4x^2 +4x+1)a^2 )/a^2 ) =6x^2 +6x+2=6(x+(1/2))^2 +(1/2) f((((√(1349))−1)/2))=6(((√(1349))/2))^2 +(1/2) =((3×1349+1)/2)=2024✓

$${AD}^{\mathrm{2}} =\left({x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{a}\left({x}+\mathrm{1}\right){q}×\frac{{q}}{{a}} \\ $$$$\:\:\:\:\:=\left({x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} −{q}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$${similarly} \\ $$$${AE}^{\mathrm{2}} =\left({x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} −{p}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$${AD}^{\mathrm{2}} +{AE}^{\mathrm{2}} =\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:=\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} −{a}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:=\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right){a}^{\mathrm{2}} \\ $$$${DE}^{\mathrm{2}} =\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} {a}^{\mathrm{2}} =\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\right){a}^{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right){a}^{\mathrm{2}} +\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\right){a}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\mathrm{6}{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{2}=\mathrm{6}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\frac{\sqrt{\mathrm{1349}}−\mathrm{1}}{\mathrm{2}}\right)=\mathrm{6}\left(\frac{\sqrt{\mathrm{1349}}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}×\mathrm{1349}+\mathrm{1}}{\mathrm{2}}=\mathrm{2024}\checkmark \\ $$

Commented by cortano12 last updated on 24/Mar/24

Terms of Service

Privacy Policy

Contact: info@tinkutara.com