Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 205530 by cherokeesay last updated on 23/Mar/24

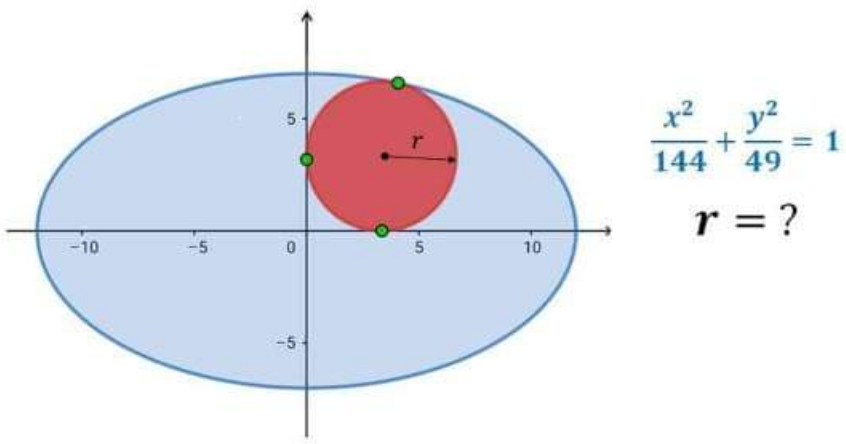
Answered by mr W last updated on 24/Mar/24

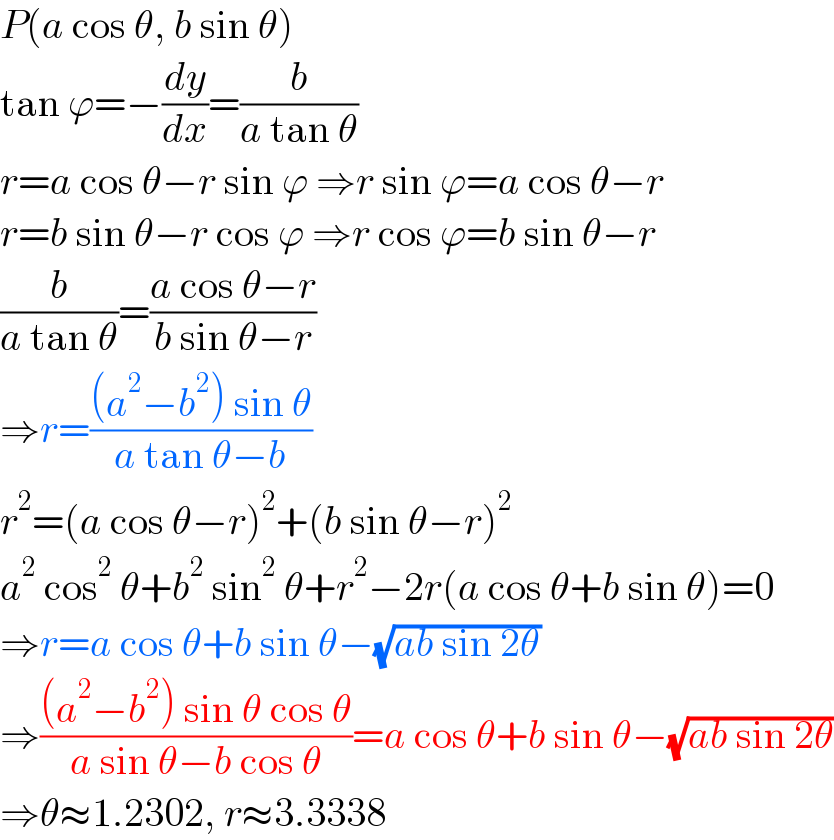
P(a cos θ, b sin θ) tan ϕ=−(dy/dx)=(b/(a tan θ)) r=a cos θ−r sin ϕ ⇒r sin ϕ=a cos θ−r r=b sin θ−r cos ϕ ⇒r cos ϕ=b sin θ−r (b/(a tan θ))=((a cos θ−r)/(b sin θ−r)) ⇒r=(((a^2 −b^2 ) sin θ)/(a tan θ−b)) r^2 =(a cos θ−r)^2 +(b sin θ−r)^2 a^2 cos^2 θ+b^2 sin^2 θ+r^2 −2r(a cos θ+b sin θ)=0 ⇒r=a cos θ+b sin θ−(√(ab sin 2θ)) ⇒(((a^2 −b^2 ) sin θ cos θ)/(a sin θ−b cos θ))=a cos θ+b sin θ−(√(ab sin 2θ)) ⇒θ≈1.2302, r≈3.3338

$${P}\left({a}\:\mathrm{cos}\:\theta,\:{b}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{tan}\:\varphi=−\frac{{dy}}{{dx}}=\frac{{b}}{{a}\:\mathrm{tan}\:\theta} \\ $$$${r}={a}\:\mathrm{cos}\:\theta−{r}\:\mathrm{sin}\:\varphi\:\Rightarrow{r}\:\mathrm{sin}\:\varphi={a}\:\mathrm{cos}\:\theta−{r} \\ $$$${r}={b}\:\mathrm{sin}\:\theta−{r}\:\mathrm{cos}\:\varphi\:\Rightarrow{r}\:\mathrm{cos}\:\varphi={b}\:\mathrm{sin}\:\theta−{r} \\ $$$$\frac{{b}}{{a}\:\mathrm{tan}\:\theta}=\frac{{a}\:\mathrm{cos}\:\theta−{r}}{{b}\:\mathrm{sin}\:\theta−{r}} \\ $$$$\Rightarrow{r}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta}{{a}\:\mathrm{tan}\:\theta−{b}} \\ $$$${r}^{\mathrm{2}} =\left({a}\:\mathrm{cos}\:\theta−{r}\right)^{\mathrm{2}} +\left({b}\:\mathrm{sin}\:\theta−{r}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+{b}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta+{r}^{\mathrm{2}} −\mathrm{2}{r}\left({a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow{r}={a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta−\sqrt{{ab}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}{{a}\:\mathrm{sin}\:\theta−{b}\:\mathrm{cos}\:\theta}={a}\:\mathrm{cos}\:\theta+{b}\:\mathrm{sin}\:\theta−\sqrt{{ab}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\theta\approx\mathrm{1}.\mathrm{2302},\:{r}\approx\mathrm{3}.\mathrm{3338} \\ $$

Commented by mr W last updated on 23/Mar/24

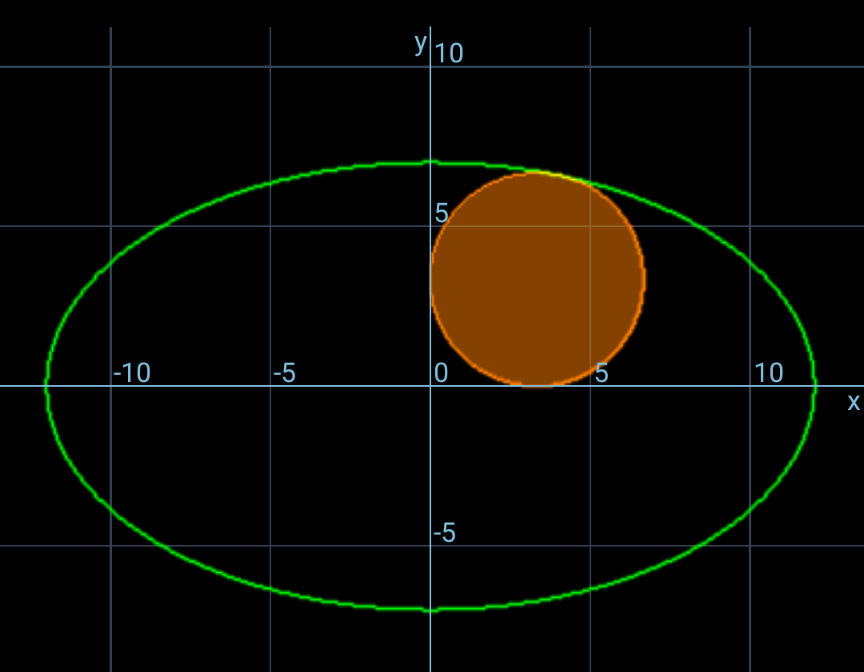
Commented by cherokeesay last updated on 23/Mar/24

thank you master !

$${thank}\:{you}\:{master}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com