
Question Number 205360 by Davidtim last updated on 18/Mar/24
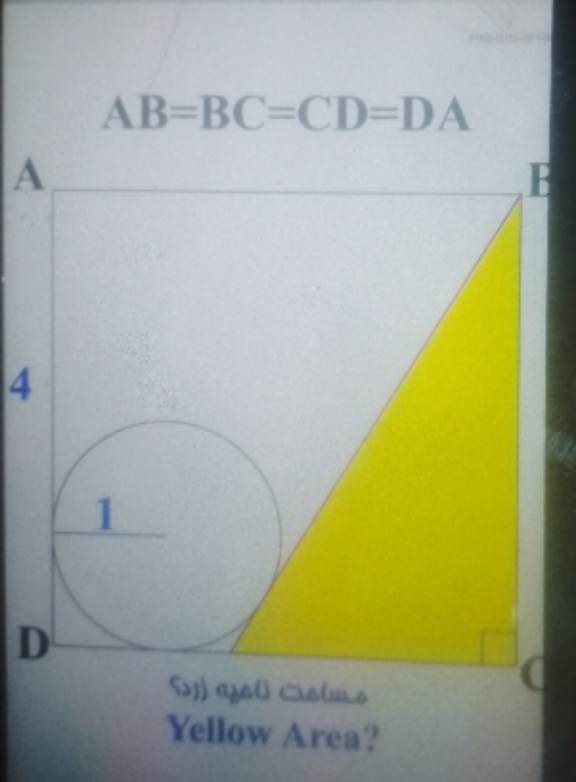
Answered by A5T last updated on 18/Mar/24
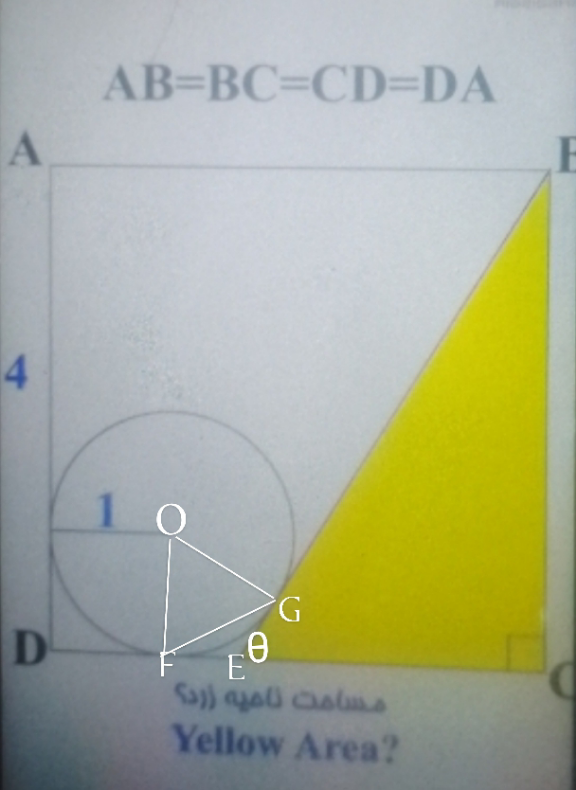
Commented by A5T last updated on 19/Mar/24

$${FE}={EG};{EB}=\sqrt{\mathrm{4}^{\mathrm{2}} +\left(\mathrm{3}−{FE}\right)^{\mathrm{2}} } \\ $$$$\angle{FEG}=\mathrm{180}-\theta\Rightarrow\angle{FOG}=\theta\:\left({since}\:{OFEG}\:{is}\:{cyclic}\right) \\ $$$$\Rightarrow{cos}\theta=\frac{\mathrm{3}−{FE}}{\:\sqrt{\mathrm{25}−\mathrm{6}{FE}+{FE}^{\mathrm{2}} }} \\ $$$${FG}^{\mathrm{2}} =\mathrm{2}{FE}^{\mathrm{2}} \left(\mathrm{1}−{cos}\left(\mathrm{180}−\theta\right)\right)=\mathrm{2}{FE}^{\mathrm{2}} \left(\mathrm{1}+{cos}\theta\right) \\ $$$${FG}^{\mathrm{2}} =\mathrm{1}+\mathrm{1}−\mathrm{2}{cos}\theta \\ $$$$\Rightarrow\mathrm{2}−\mathrm{2}{cos}\theta=\mathrm{2}{FE}^{\mathrm{2}} \left(\mathrm{1}+{cos}\theta\right)\Rightarrow\mathrm{1}−{cos}\theta={FE}^{\mathrm{2}} +{FE}^{\mathrm{2}} {cos}\theta \\ $$$$\Rightarrow\mathrm{1}−{FE}^{\mathrm{2}} ={cos}\theta\left(\mathrm{1}+{FE}^{\mathrm{2}} \right)\Rightarrow{cos}\theta=\frac{\mathrm{1}−{FE}^{\mathrm{2}} }{\mathrm{1}+{FE}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}−{FE}^{\mathrm{2}} }{\mathrm{1}+{FE}^{\mathrm{2}} }=\frac{\mathrm{3}−{FE}}{\:\sqrt{\mathrm{25}−\mathrm{6}{FE}+{FE}^{\mathrm{2}} }}\Rightarrow{FE}=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}}={EG} \\ $$$${AO}=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{10}\:}\wedge\:{sinDAO}=\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}={cos}\left(\mathrm{90}−{DAO}\right) \\ $$$${OB}^{\mathrm{2}} ={AO}^{\mathrm{2}} +{AB}^{\mathrm{2}} −\mathrm{2}{AO}×{ABcos}\left(\mathrm{90}−{DAO}\right) \\ $$$$\Rightarrow{OB}^{\mathrm{2}} =\mathrm{10}+\mathrm{16}−\mathrm{2}×\mathrm{4}=\mathrm{18}\Rightarrow{OB}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{GB}=\sqrt{{OB}^{\mathrm{2}} −{OG}^{\mathrm{2}} }=\sqrt{\mathrm{18}−\mathrm{1}}=\sqrt{\mathrm{17}} \\ $$$$\Rightarrow{BE}={EG}+{BG}=\frac{\mathrm{3}\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}}\Rightarrow{BE}^{\mathrm{2}} =\frac{\mathrm{162}−\mathrm{18}\sqrt{\mathrm{17}}}{\mathrm{4}} \\ $$$$\Rightarrow{EC}=\sqrt{{BE}^{\mathrm{2}} −{BC}^{\mathrm{2}} }=\sqrt{\frac{\mathrm{98}−\mathrm{18}\sqrt{\mathrm{17}}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{98}−\mathrm{18}\sqrt{\mathrm{17}}}}{\mathrm{2}} \\ $$$$\Rightarrow{Yellow}\:{Area}=\frac{{EC}×{BC}}{\mathrm{2}}=\sqrt{\mathrm{98}−\mathrm{18}\sqrt{\mathrm{17}}}\:{sq}.\:{units} \\ $$
Commented by Davidtim last updated on 19/Mar/24
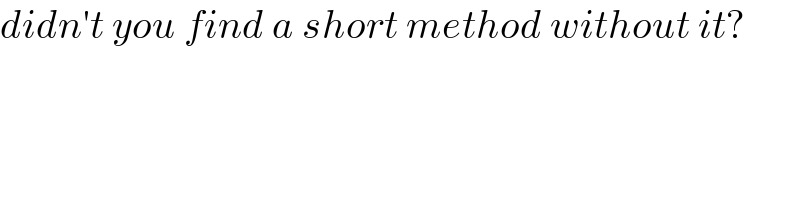
$${didn}'{t}\:{you}\:{find}\:{a}\:{short}\:{method}\:{without}\:{it}? \\ $$
Commented by A5T last updated on 19/Mar/24
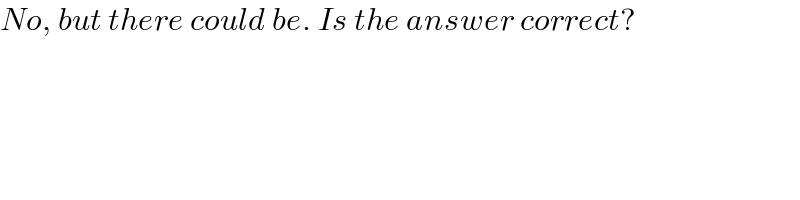
$${No},\:{but}\:{there}\:{could}\:{be}.\:{Is}\:{the}\:{answer}\:{correct}? \\ $$
Commented by mr W last updated on 19/Mar/24

$$\sqrt{\mathrm{98}−\mathrm{18}\sqrt{\mathrm{17}}}=\mathrm{9}−\sqrt{\mathrm{17}} \\ $$
Commented by A5T last updated on 19/Mar/24

$${Yea}\checkmark \\ $$
Answered by mr W last updated on 20/Mar/24
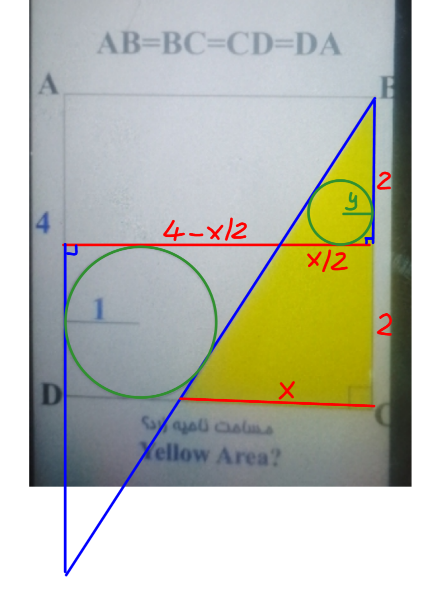
Commented by mr W last updated on 19/Mar/24
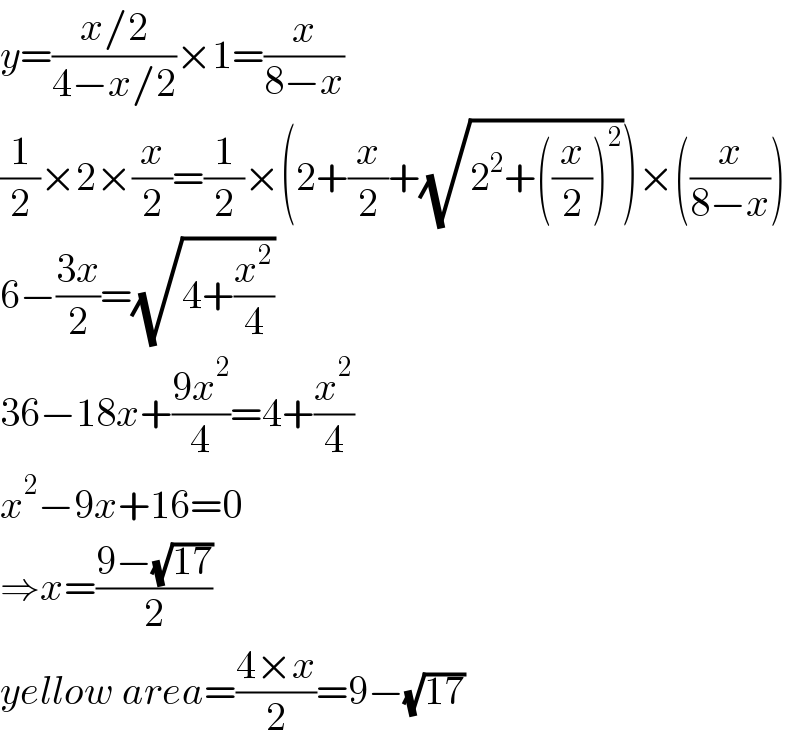
$${y}=\frac{{x}/\mathrm{2}}{\mathrm{4}−{x}/\mathrm{2}}×\mathrm{1}=\frac{{x}}{\mathrm{8}−{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\frac{{x}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{2}+\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{2}^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }\right)×\left(\frac{{x}}{\mathrm{8}−{x}}\right) \\ $$$$\mathrm{6}−\frac{\mathrm{3}{x}}{\mathrm{2}}=\sqrt{\mathrm{4}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\mathrm{36}−\mathrm{18}{x}+\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{4}+\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{9}−\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$${yellow}\:{area}=\frac{\mathrm{4}×{x}}{\mathrm{2}}=\mathrm{9}−\sqrt{\mathrm{17}} \\ $$
