Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 205334 by cortano12 last updated on 17/Mar/24

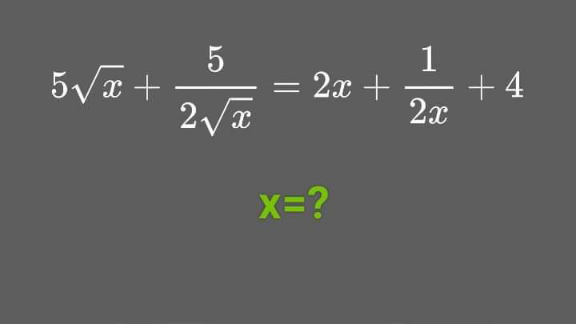
Commented by Ghisom last updated on 17/Mar/24

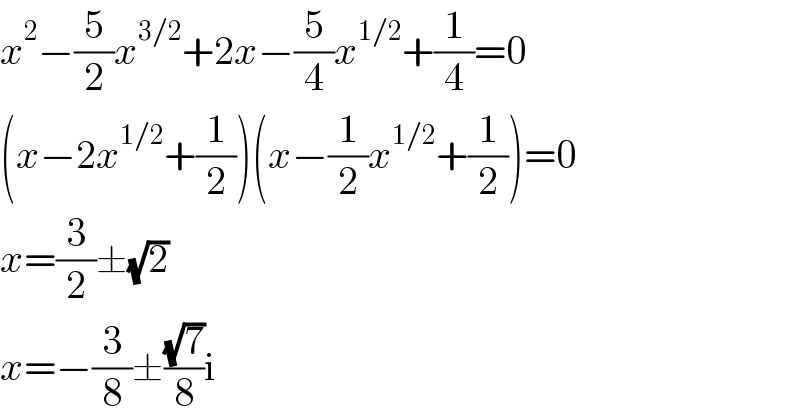
x^2 −(5/2)x^(3/2) +2x−(5/4)x^(1/2) +(1/4)=0 (x−2x^(1/2) +(1/2))(x−(1/2)x^(1/2) +(1/2))=0 x=(3/2)±(√2) x=−(3/8)±((√7)/8)i

$${x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}{x}^{\mathrm{3}/\mathrm{2}} +\mathrm{2}{x}−\frac{\mathrm{5}}{\mathrm{4}}{x}^{\mathrm{1}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}{x}^{\mathrm{1}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{1}/\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\mathrm{2}} \\ $$$${x}=−\frac{\mathrm{3}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{7}}}{\mathrm{8}}\mathrm{i} \\ $$

Answered by Rasheed.Sindhi last updated on 17/Mar/24

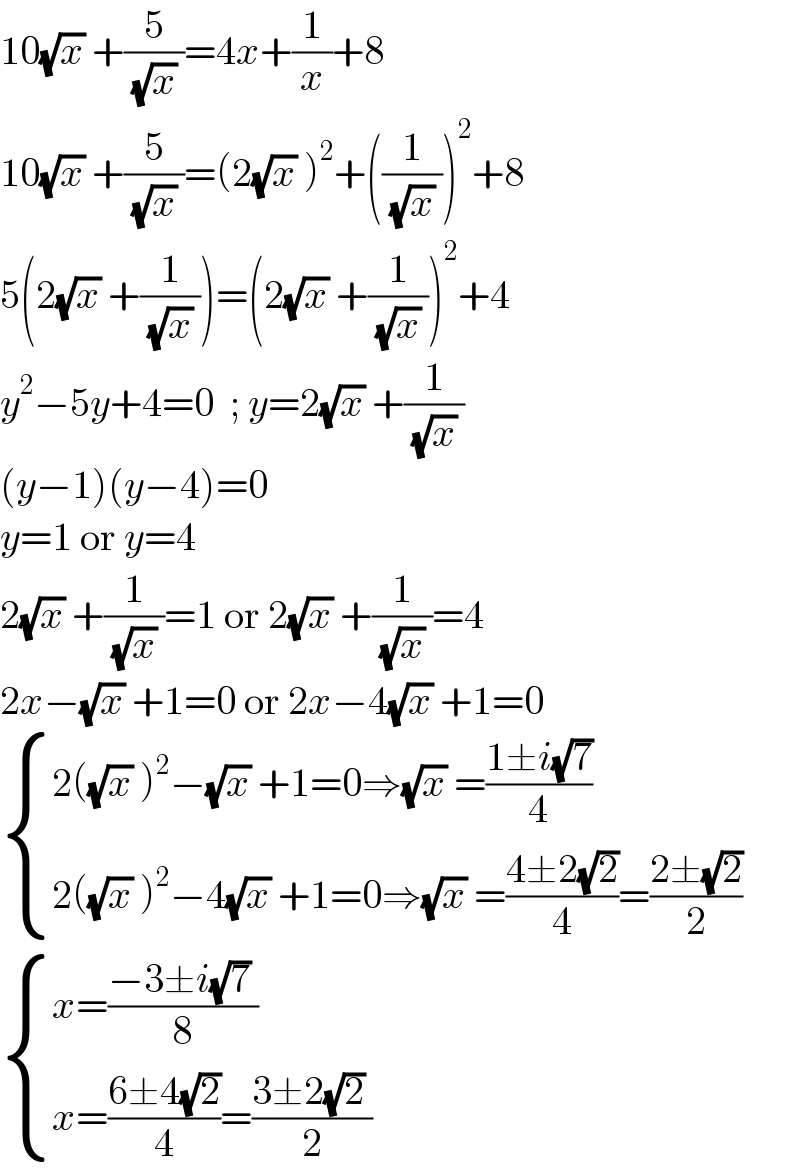
10(√x) +(5/( (√x) ))=4x+(1/x)+8 10(√x) +(5/( (√x) ))=(2(√x) )^2 +((1/( (√x) )))^2 +8 5(2(√x) +(1/( (√x) )))=(2(√x) +(1/( (√x) )))^2 +4 y^2 −5y+4=0 ; y=2(√x) +(1/( (√x) )) (y−1)(y−4)=0 y=1 or y=4 2(√x) +(1/( (√x) ))=1 or 2(√x) +(1/( (√x) ))=4 2x−(√x) +1=0 or 2x−4(√x) +1=0 { ((2((√x) )^2 −(√x) +1=0⇒(√x) =((1±i(√7))/4))),((2((√x) )^2 −4(√x) +1=0⇒(√x) =((4±2(√2))/4)=((2±(√2))/2))) :} { ((x=((−3±i(√7) )/8))),((x=((6±4(√2))/4)=((3±2(√2) )/2))) :}

$$\mathrm{10}\sqrt{{x}}\:+\frac{\mathrm{5}}{\:\sqrt{{x}}\:}=\mathrm{4}{x}+\frac{\mathrm{1}}{{x}}+\mathrm{8} \\ $$$$\mathrm{10}\sqrt{{x}}\:+\frac{\mathrm{5}}{\:\sqrt{{x}}\:}=\left(\mathrm{2}\sqrt{{x}}\:\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\right)^{\mathrm{2}} +\mathrm{8} \\ $$$$\mathrm{5}\left(\mathrm{2}\sqrt{{x}}\:+\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\right)=\left(\mathrm{2}\sqrt{{x}}\:+\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\right)^{\mathrm{2}} +\mathrm{4} \\ $$$${y}^{\mathrm{2}} −\mathrm{5}{y}+\mathrm{4}=\mathrm{0}\:\:;\:{y}=\mathrm{2}\sqrt{{x}}\:+\frac{\mathrm{1}}{\:\sqrt{{x}}\:} \\ $$$$\left({y}−\mathrm{1}\right)\left({y}−\mathrm{4}\right)=\mathrm{0} \\ $$$${y}=\mathrm{1}\:\mathrm{or}\:{y}=\mathrm{4} \\ $$$$\mathrm{2}\sqrt{{x}}\:+\frac{\mathrm{1}}{\:\sqrt{{x}}\:}=\mathrm{1}\:\mathrm{or}\:\mathrm{2}\sqrt{{x}}\:+\frac{\mathrm{1}}{\:\sqrt{{x}}\:}=\mathrm{4} \\ $$$$\mathrm{2}{x}−\sqrt{{x}}\:+\mathrm{1}=\mathrm{0}\:\mathrm{or}\:\mathrm{2}{x}−\mathrm{4}\sqrt{{x}}\:+\mathrm{1}=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{2}\left(\sqrt{{x}}\:\right)^{\mathrm{2}} −\sqrt{{x}}\:+\mathrm{1}=\mathrm{0}\Rightarrow\sqrt{{x}}\:=\frac{\mathrm{1}\pm{i}\sqrt{\mathrm{7}}}{\mathrm{4}}}\\{\mathrm{2}\left(\sqrt{{x}}\:\right)^{\mathrm{2}} −\mathrm{4}\sqrt{{x}}\:+\mathrm{1}=\mathrm{0}\Rightarrow\sqrt{{x}}\:=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\mathrm{2}\pm\sqrt{\mathrm{2}}}{\mathrm{2}}}\end{cases}\: \\ $$$$\begin{cases}{{x}=\frac{−\mathrm{3}\pm{i}\sqrt{\mathrm{7}}\:}{\mathrm{8}}}\\{{x}=\frac{\mathrm{6}\pm\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{2}}\:}{\mathrm{2}}}\end{cases} \\ $$

Commented by Rasheed.Sindhi last updated on 17/Mar/24

Corrected sir

$${Corrected}\:{sir} \\ $$

Commented by cortano12 last updated on 17/Mar/24

10(√x) +(5/( (√x))) = 4x+(1/x)+8

$$\:\mathrm{10}\sqrt{\mathrm{x}}\:+\frac{\mathrm{5}}{\:\sqrt{\mathrm{x}}}\:=\:\mathrm{4x}+\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{8}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com