
Question Number 205237 by universe last updated on 13/Mar/24
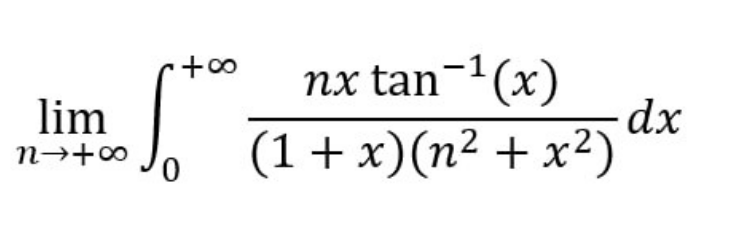
Answered by Berbere last updated on 13/Mar/24
![n^2 +x^2 ≥n^2 (x/(1+x))≤1⇒((nxtan^(−1) (x))/((1+x)(n^2 +x^2 )))≤n.1.((tan^(−1) (x))/(n^2 +x^2 ))=n((tan^(−1) (x))/(n^2 +x^2 )) ⇒∫_0 ^∞ ((nxtan^(−1) (x))/((1+x)(n^2 +x^2 )))dx≤∫_0 ^∞ n((tan^(−1) (x))/(n^2 +x^2 ))≤((nπ)/2)∫_0 ^∞ (dx/(n^2 +x^2 )) =((nπ)/2)[(1/n)tan^(−1) ((x/n))]_0 ^∞ =(π^2 /4) we can exchange ∫ and lim ⇒lim_(n→∞) ∫_0 ^∞ ((nxtan^(−1) (x))/((1+x)(n^2 +x^2 )))dx=∫_0 ^∞ lim_(n→∞) ((xtan^(−1) (x))/(1+x))(n/(n^2 +x^2 ))dx=0](Q205243.png)
$${n}^{\mathrm{2}} +{x}^{\mathrm{2}} \geqslant{n}^{\mathrm{2}} \\ $$$$\frac{{x}}{\mathrm{1}+{x}}\leqslant\mathrm{1}\Rightarrow\frac{{nx}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\left(\mathrm{1}+{x}\right)\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}\leqslant{n}.\mathrm{1}.\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} }={n}\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{nx}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\left(\mathrm{1}+{x}\right)\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}{dx}\leqslant\int_{\mathrm{0}} ^{\infty} {n}\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} }\leqslant\frac{{n}\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$=\frac{{n}\pi}{\mathrm{2}}\left[\frac{\mathrm{1}}{{n}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{x}}{{n}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$${we}\:{can}\:{exchange}\:\int\:{and}\:{lim} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \frac{{nx}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\left(\mathrm{1}+{x}\right)\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}{dx}=\int_{\mathrm{0}} ^{\infty} \underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\mathrm{1}+{x}}\frac{{n}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}=\mathrm{0} \\ $$
Commented by universe last updated on 13/Mar/24

$${thanks}\:{sir} \\ $$
Commented by Berbere last updated on 13/Mar/24

$${withe}\:{Pleasur} \\ $$
