Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 205062 by BaliramKumar last updated on 07/Mar/24

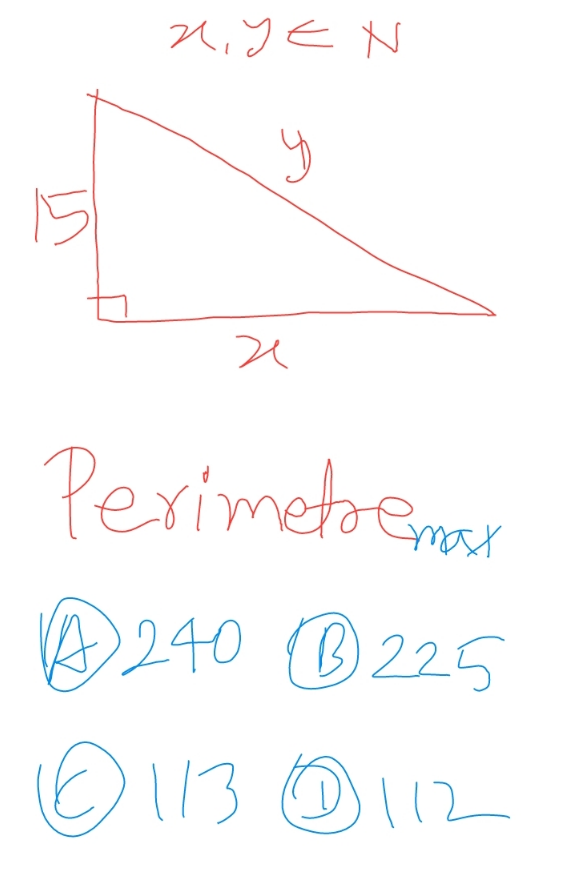
Answered by cortano12 last updated on 07/Mar/24

P_(max) = 240

$$\:\:\mathrm{P}_{\mathrm{max}} \:=\:\mathrm{240}\: \\ $$

Commented by BaliramKumar last updated on 07/Mar/24

solution

$$\mathrm{solution} \\ $$

Answered by mr W last updated on 07/Mar/24

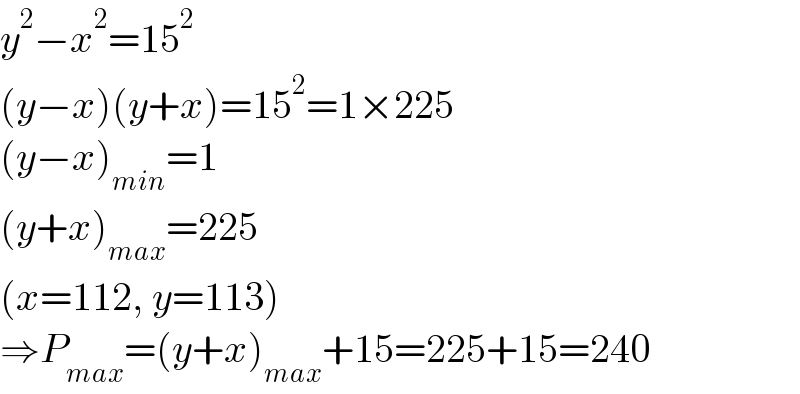
y^2 −x^2 =15^2 (y−x)(y+x)=15^2 =1×225 (y−x)_(min) =1 (y+x)_(max) =225 (x=112, y=113) ⇒P_(max) =(y+x)_(max) +15=225+15=240

$${y}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} \: \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)=\mathrm{15}^{\mathrm{2}} =\mathrm{1}×\mathrm{225} \\ $$$$\left({y}−{x}\right)_{{min}} =\mathrm{1} \\ $$$$\left({y}+{x}\right)_{{max}} =\mathrm{225} \\ $$$$\left({x}=\mathrm{112},\:{y}=\mathrm{113}\right) \\ $$$$\Rightarrow{P}_{{max}} =\left({y}+{x}\right)_{{max}} +\mathrm{15}=\mathrm{225}+\mathrm{15}=\mathrm{240} \\ $$

Commented by BaliramKumar last updated on 07/Mar/24

thanks

$$\mathrm{thanks} \\ $$

Answered by Rasheed.Sindhi last updated on 07/Mar/24

If a,b∈N with a>b then a^2 −b^2 , 2ab , a^2 +b^2 are sides of right triangle i-e pathagorean triple. 2ab is certainly an even number and a^2 +b^2 is hypotenuse. Hence a^2 −b^2 =15 (a−b)(a+b)=1×3×5 { ((a−b=1 ∧ a+b=15⇒(a,b)=(8,7))),((a−b=3 ∧ a+b=5⇒(a,b)=(4,1))) :} determinant ((a,b,(a^2 −b^2 ),(2ab),(a^2 +b^2 ),(perimeter)),(8,7,(15),(112),(113),(240)),(4,1,(15),8,(17),(40))) The above formula works only for primitive triples.To find out non- primitive triples we can use this same formula to find out primitive triples, first, with one side 3 or 5: a^2 −b^2 =3⇒(a−b)(a+b)=1×3 a−b=1∧ a+b=3⇒(a,b)=(2,1) a^2 −b^2 =5⇒(a−b)(a+b)=1×5 a−b=1∧ a+b=5⇒(a,b)=(3,2) determinant ((a,b,(a^2 −b^2 ),(2ab),(a^2 +b^2 )),(2,1,3,4,5),(3,2,5,(12),(13))) (3,4,5)×5=(15,20,25)⇒p=60 (5,12,13)×3=(15,36,39)⇒p=80 Yet the max p=240

$${If}\:{a},{b}\in\mathbb{N}\:{with}\:{a}>{b}\:{then} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ,\:\mathrm{2}{ab}\:,\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:{are}\:{sides}\:{of} \\ $$$$\boldsymbol{{right}}\:\boldsymbol{{triangle}}\:{i}-{e}\:{pathagorean} \\ $$$${triple}. \\ $$$$\mathrm{2}{ab}\:{is}\:{certainly}\:{an}\:{even}\:{number} \\ $$$${and}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:{is}\:{hypotenuse}.\:{Hence} \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{15} \\ $$$$\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{1}×\mathrm{3}×\mathrm{5} \\ $$$$\begin{cases}{{a}−{b}=\mathrm{1}\:\wedge\:{a}+{b}=\mathrm{15}\Rightarrow\left({a},{b}\right)=\left(\mathrm{8},\mathrm{7}\right)}\\{{a}−{b}=\mathrm{3}\:\wedge\:{a}+{b}=\mathrm{5}\Rightarrow\left({a},{b}\right)=\left(\mathrm{4},\mathrm{1}\right)}\end{cases} \\ $$$$\begin{array}{|c|c|c|}{{a}}&\hline{{b}}&\hline{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }&\hline{\mathrm{2}{ab}}&\hline{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }&\hline{{perimeter}}\\{\mathrm{8}}&\hline{\mathrm{7}}&\hline{\mathrm{15}}&\hline{\mathrm{112}}&\hline{\mathrm{113}}&\hline{\mathrm{240}}\\{\mathrm{4}}&\hline{\mathrm{1}}&\hline{\mathrm{15}}&\hline{\mathrm{8}}&\hline{\mathrm{17}}&\hline{\mathrm{40}}\\\hline\end{array}\: \\ $$$$\boldsymbol{\mathrm{The}}\:\boldsymbol{\mathrm{above}}\:\boldsymbol{\mathrm{formula}}\:\boldsymbol{\mathrm{works}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{for}} \\ $$$$\boldsymbol{\mathrm{primitive}}\:\boldsymbol{\mathrm{triples}}.\boldsymbol{\mathrm{To}}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{out}}\:\boldsymbol{\mathrm{non}}- \\ $$$$\boldsymbol{\mathrm{primitive}}\:\boldsymbol{\mathrm{triples}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{this}} \\ $$$$\boldsymbol{\mathrm{same}}\:\boldsymbol{\mathrm{formula}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{out}}\:\boldsymbol{\mathrm{primitive}} \\ $$$$\boldsymbol{\mathrm{triples}},\:\boldsymbol{\mathrm{first}},\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{one}}\:\boldsymbol{\mathrm{side}}\:\mathrm{3}\:\boldsymbol{\mathrm{or}}\:\mathrm{5}: \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{3}\Rightarrow\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{1}×\mathrm{3} \\ $$$$\:\:\:{a}−{b}=\mathrm{1}\wedge\:{a}+{b}=\mathrm{3}\Rightarrow\left({a},{b}\right)=\left(\mathrm{2},\mathrm{1}\right) \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{5}\Rightarrow\left({a}−{b}\right)\left({a}+{b}\right)=\mathrm{1}×\mathrm{5} \\ $$$$\:\:\:{a}−{b}=\mathrm{1}\wedge\:{a}+{b}=\mathrm{5}\Rightarrow\left({a},{b}\right)=\left(\mathrm{3},\mathrm{2}\right) \\ $$$$\begin{array}{|c|c|c|}{{a}}&\hline{{b}}&\hline{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }&\hline{\mathrm{2}{ab}}&\hline{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\\{\mathrm{2}}&\hline{\mathrm{1}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\mathrm{5}}\\{\mathrm{3}}&\hline{\mathrm{2}}&\hline{\mathrm{5}}&\hline{\mathrm{12}}&\hline{\mathrm{13}}\\\hline\end{array} \\ $$$$\left(\mathrm{3},\mathrm{4},\mathrm{5}\right)×\mathrm{5}=\left(\mathrm{15},\mathrm{20},\mathrm{25}\right)\Rightarrow{p}=\mathrm{60} \\ $$$$\left(\mathrm{5},\mathrm{12},\mathrm{13}\right)×\mathrm{3}=\left(\mathrm{15},\mathrm{36},\mathrm{39}\right)\Rightarrow{p}=\mathrm{80}\: \\ $$$${Yet}\:{the}\:{max}\:{p}=\mathrm{240} \\ $$

Commented by BaliramKumar last updated on 07/Mar/24

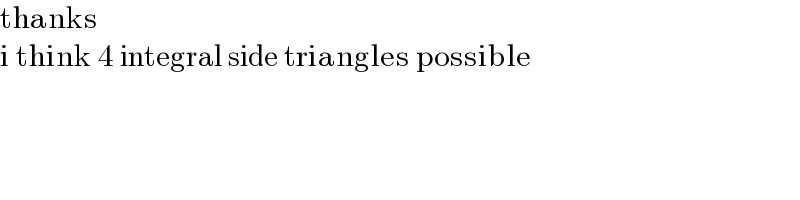
thanks i think 4 integral side triangles possible

$$\mathrm{thanks} \\ $$$$\mathrm{i}\:\mathrm{think}\:\mathrm{4}\:\mathrm{integral}\:\mathrm{side}\:\mathrm{triangles}\:\mathrm{possible} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 07/Mar/24

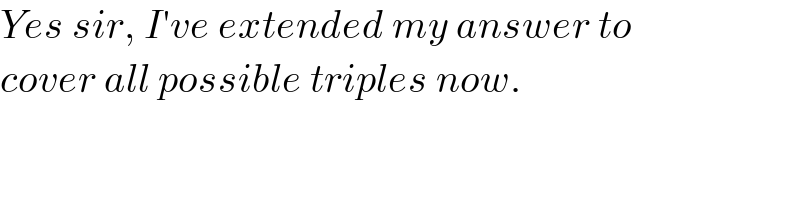
Yes sir, I′ve extended my answer to cover all possible triples now.

$${Yes}\:{sir},\:{I}'{ve}\:{extended}\:{my}\:{answer}\:{to} \\ $$$${cover}\:{all}\:{possible}\:{triples}\:{now}. \\ $$

Commented by BaliramKumar last updated on 07/Mar/24

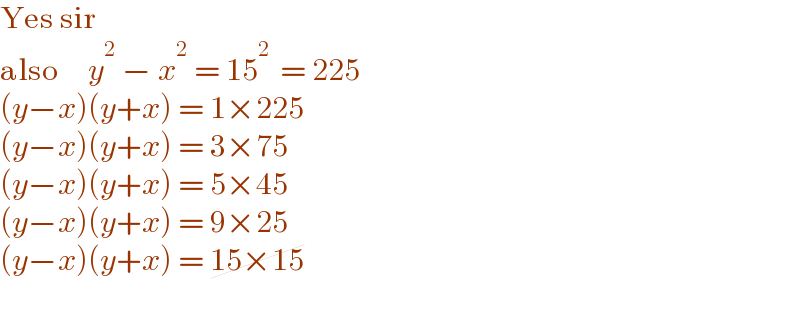
Yes sir also y^2 − x^2 = 15^(2 ) = 225 (y−x)(y+x) = 1×225 (y−x)(y+x) = 3×75 (y−x)(y+x) = 5×45 (y−x)(y+x) = 9×25 (y−x)(y+x) = 15×15

$$\mathrm{Yes}\:\mathrm{sir} \\ $$$$\mathrm{also}\:\:\:\:\:{y}^{\mathrm{2}} \:−\:{x}^{\mathrm{2}} \:=\:\mathrm{15}^{\mathrm{2}\:} \:=\:\mathrm{225} \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)\:=\:\mathrm{1}×\mathrm{225} \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)\:=\:\mathrm{3}×\mathrm{75} \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)\:=\:\mathrm{5}×\mathrm{45} \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)\:=\:\mathrm{9}×\mathrm{25} \\ $$$$\left({y}−{x}\right)\left({y}+{x}\right)\:=\:\cancel{\mathrm{15}×\mathrm{15}} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 08/Mar/24

An easy way!

$${An}\:{easy}\:{way}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com