Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 204418 by peter frank last updated on 17/Feb/24

Commented by mr W last updated on 19/Feb/24

y=2(x−(1/x))^2

$${y}=\mathrm{2}\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$

Answered by mr W last updated on 19/Feb/24

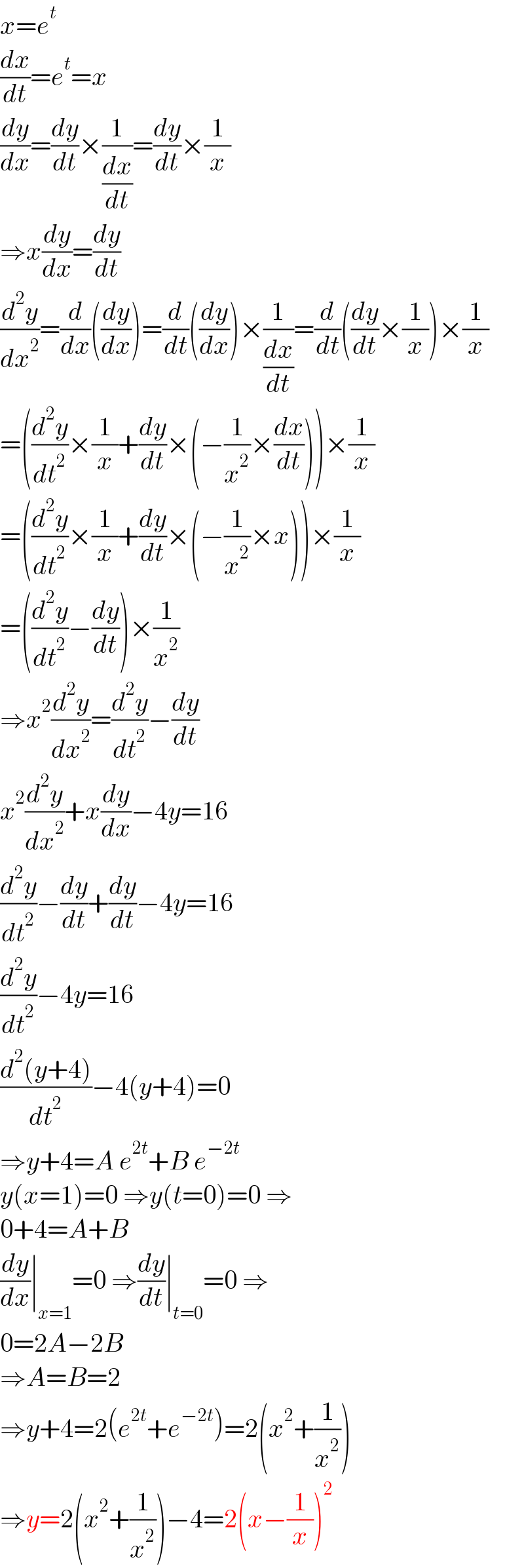
x=e^t (dx/dt)=e^t =x (dy/dx)=(dy/dt)×(1/(dx/dt))=(dy/dt)×(1/x) ⇒x(dy/dx)=(dy/dt) (d^2 y/dx^2 )=(d/dx)((dy/dx))=(d/dt)((dy/dx))×(1/(dx/dt))=(d/dt)((dy/dt)×(1/x))×(1/x) =((d^2 y/dt^2 )×(1/x)+(dy/dt)×(−(1/x^2 )×(dx/dt)))×(1/x) =((d^2 y/dt^2 )×(1/x)+(dy/dt)×(−(1/x^2 )×x))×(1/x) =((d^2 y/dt^2 )−(dy/dt))×(1/x^2 ) ⇒x^2 (d^2 y/dx^2 )=(d^2 y/dt^2 )−(dy/dt) x^2 (d^2 y/dx^2 )+x(dy/dx)−4y=16 (d^2 y/dt^2 )−(dy/dt)+(dy/dt)−4y=16 (d^2 y/dt^2 )−4y=16 ((d^2 (y+4))/dt^2 )−4(y+4)=0 ⇒y+4=A e^(2t) +B e^(−2t) y(x=1)=0 ⇒y(t=0)=0 ⇒ 0+4=A+B (dy/dx)∣_(x=1) =0 ⇒(dy/dt)∣_(t=0) =0 ⇒ 0=2A−2B ⇒A=B=2 ⇒y+4=2(e^(2t) +e^(−2t) )=2(x^2 +(1/x^2 )) ⇒y=2(x^2 +(1/x^2 ))−4=2(x−(1/x))^2

$${x}={e}^{{t}} \\ $$$$\frac{{dx}}{{dt}}={e}^{{t}} ={x} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}×\frac{\mathrm{1}}{\frac{{dx}}{{dt}}}=\frac{{dy}}{{dt}}×\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{x}\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{d}}{{dt}}\left(\frac{{dy}}{{dx}}\right)×\frac{\mathrm{1}}{\frac{{dx}}{{dt}}}=\frac{{d}}{{dt}}\left(\frac{{dy}}{{dt}}×\frac{\mathrm{1}}{{x}}\right)×\frac{\mathrm{1}}{{x}} \\ $$$$=\left(\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }×\frac{\mathrm{1}}{{x}}+\frac{{dy}}{{dt}}×\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }×\frac{{dx}}{{dt}}\right)\right)×\frac{\mathrm{1}}{{x}} \\ $$$$=\left(\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }×\frac{\mathrm{1}}{{x}}+\frac{{dy}}{{dt}}×\left(−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }×{x}\right)\right)×\frac{\mathrm{1}}{{x}} \\ $$$$=\left(\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}}\right)×\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}} \\ $$$${x}^{\mathrm{2}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+{x}\frac{{dy}}{{dx}}−\mathrm{4}{y}=\mathrm{16} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\frac{{dy}}{{dt}}+\frac{{dy}}{{dt}}−\mathrm{4}{y}=\mathrm{16} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }−\mathrm{4}{y}=\mathrm{16} \\ $$$$\frac{{d}^{\mathrm{2}} \left({y}+\mathrm{4}\right)}{{dt}^{\mathrm{2}} }−\mathrm{4}\left({y}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{y}+\mathrm{4}={A}\:{e}^{\mathrm{2}{t}} +{B}\:{e}^{−\mathrm{2}{t}} \\ $$$${y}\left({x}=\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{y}\left({t}=\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{0}+\mathrm{4}={A}+{B} \\ $$$$\frac{{dy}}{{dx}}\mid_{{x}=\mathrm{1}} =\mathrm{0}\:\Rightarrow\frac{{dy}}{{dt}}\mid_{{t}=\mathrm{0}} =\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{0}=\mathrm{2}{A}−\mathrm{2}{B} \\ $$$$\Rightarrow{A}={B}=\mathrm{2} \\ $$$$\Rightarrow{y}+\mathrm{4}=\mathrm{2}\left({e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} \right)=\mathrm{2}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{y}=\mathrm{2}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{4}=\mathrm{2}\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} \\ $$

Commented by peter frank last updated on 21/Feb/24

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com