Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 204197 by ajfour last updated on 08/Feb/24

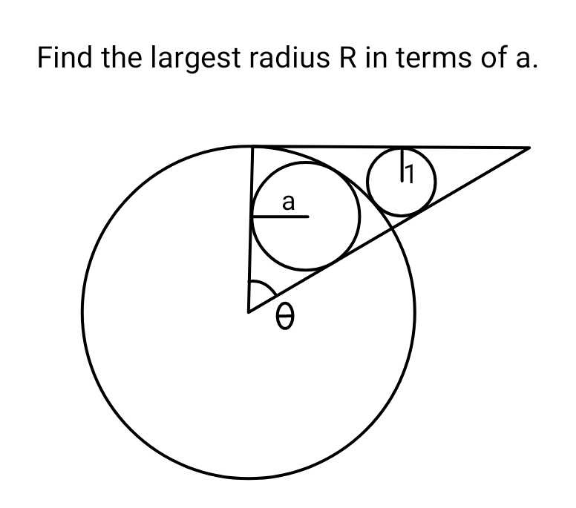
Answered by mr W last updated on 08/Feb/24

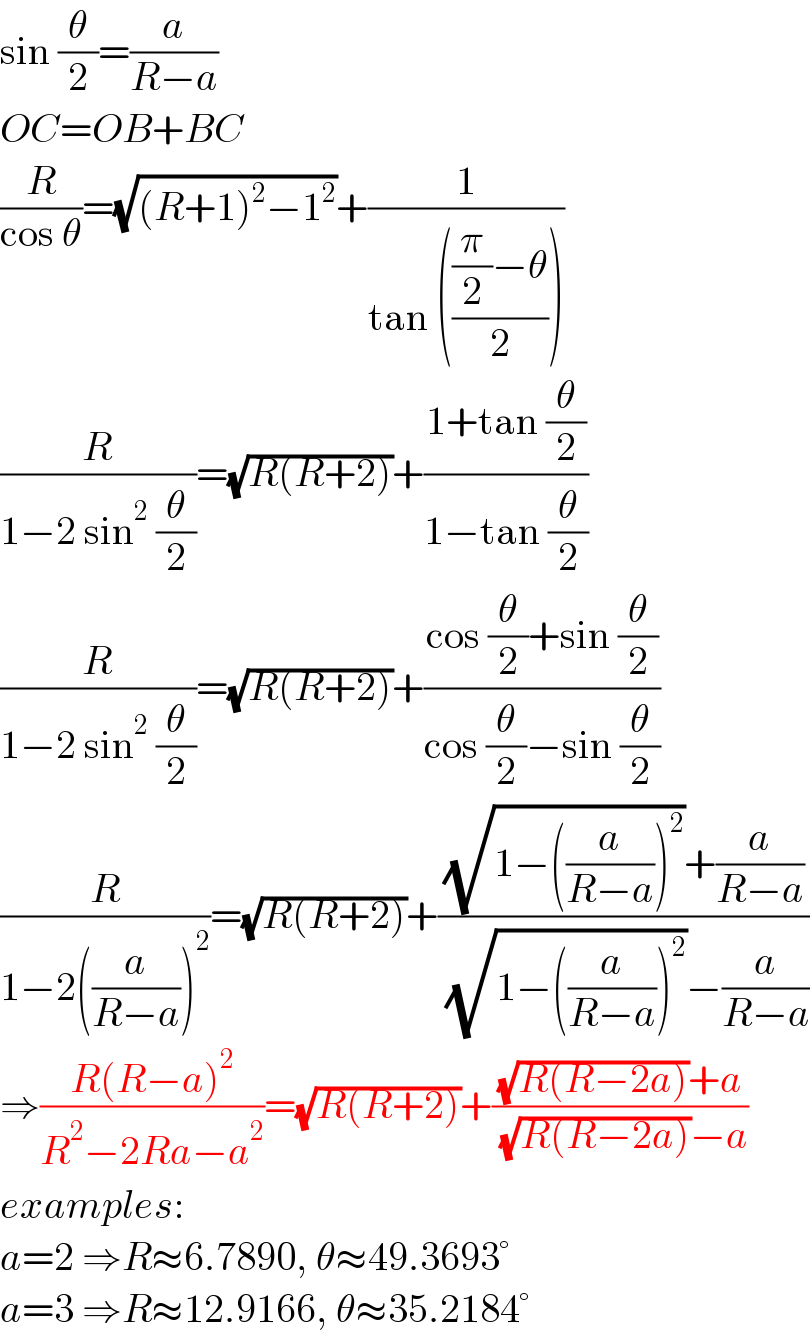
sin (θ/2)=(a/(R−a)) OC=OB+BC (R/(cos θ))=(√((R+1)^2 −1^2 ))+(1/(tan ((((π/2)−θ)/2)))) (R/(1−2 sin^2 (θ/2)))=(√(R(R+2)))+((1+tan (θ/2))/(1−tan (θ/2))) (R/(1−2 sin^2 (θ/2)))=(√(R(R+2)))+((cos (θ/2)+sin (θ/2))/(cos (θ/2)−sin (θ/2))) (R/(1−2((a/(R−a)))^2 ))=(√(R(R+2)))+(((√(1−((a/(R−a)))^2 ))+(a/(R−a)))/( (√(1−((a/(R−a)))^2 ))−(a/(R−a)))) ⇒((R(R−a)^2 )/(R^2 −2Ra−a^2 ))=(√(R(R+2)))+(((√(R(R−2a)))+a)/( (√(R(R−2a)))−a)) examples: a=2 ⇒R≈6.7890, θ≈49.3693° a=3 ⇒R≈12.9166, θ≈35.2184°

$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{a}}{{R}−{a}} \\ $$$${OC}={OB}+{BC} \\ $$$$\frac{{R}}{\mathrm{cos}\:\theta}=\sqrt{\left({R}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\frac{\pi}{\mathrm{2}}−\theta}{\mathrm{2}}\right)} \\ $$$$\frac{{R}}{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\sqrt{{R}\left({R}+\mathrm{2}\right)}+\frac{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\frac{{R}}{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=\sqrt{{R}\left({R}+\mathrm{2}\right)}+\frac{\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\frac{{R}}{\mathrm{1}−\mathrm{2}\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} }=\sqrt{{R}\left({R}+\mathrm{2}\right)}+\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} }+\frac{{a}}{{R}−{a}}}{\:\sqrt{\mathrm{1}−\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} }−\frac{{a}}{{R}−{a}}} \\ $$$$\Rightarrow\frac{{R}\left({R}−{a}\right)^{\mathrm{2}} }{{R}^{\mathrm{2}} −\mathrm{2}{Ra}−{a}^{\mathrm{2}} }=\sqrt{{R}\left({R}+\mathrm{2}\right)}+\frac{\sqrt{{R}\left({R}−\mathrm{2}{a}\right)}+{a}}{\:\sqrt{{R}\left({R}−\mathrm{2}{a}\right)}−{a}} \\ $$$${examples}: \\ $$$${a}=\mathrm{2}\:\Rightarrow{R}\approx\mathrm{6}.\mathrm{7890},\:\theta\approx\mathrm{49}.\mathrm{3693}° \\ $$$${a}=\mathrm{3}\:\Rightarrow{R}\approx\mathrm{12}.\mathrm{9166},\:\theta\approx\mathrm{35}.\mathrm{2184}° \\ $$

Commented by mr W last updated on 08/Feb/24

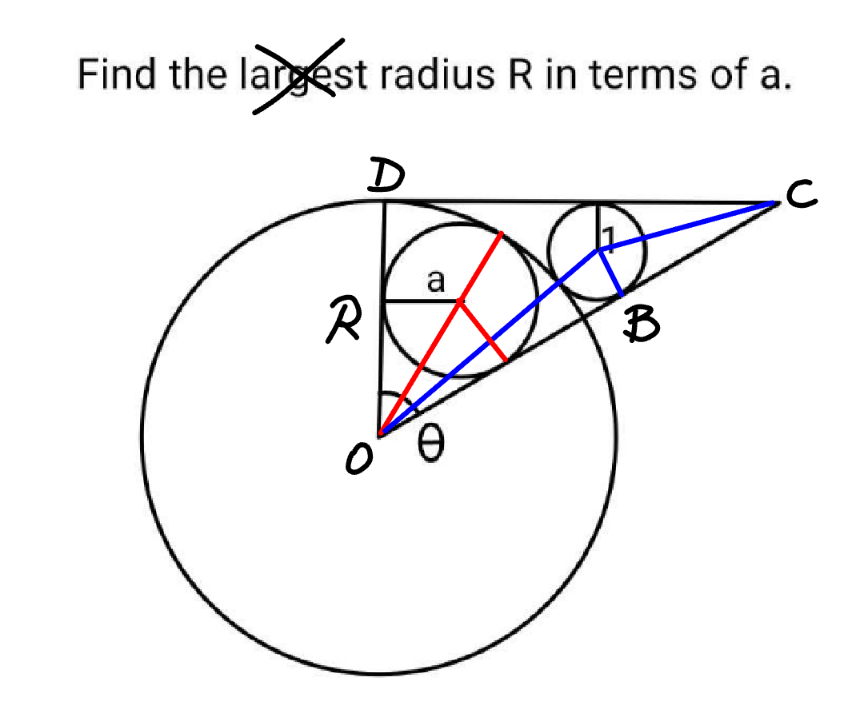
Commented by ajfour last updated on 08/Feb/24

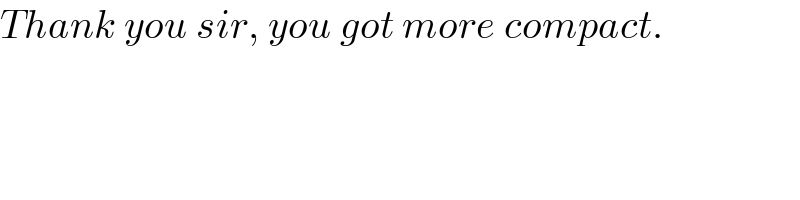
Thank you sir, you got more compact.

$${Thank}\:{you}\:{sir},\:{you}\:{got}\:{more}\:{compact}. \\ $$

Commented by mr W last updated on 08/Feb/24

thanks sir! please have a look at Q204078.

$${thanks}\:{sir}! \\ $$$${please}\:{have}\:{a}\:{look}\:{at}\:{Q}\mathrm{204078}. \\ $$

Answered by ajfour last updated on 08/Feb/24

centre of largest (here) circle be origin. y=mx line eq. m=(1/(tan θ)) at y=R, x=Rtan θ sin (θ/2)=(a/(R−a)) tan θ=(√((1/({1−2((a/(R−a)))^2 }^2 ))−1)) P[(R+1)cos φ, (R+1)sin φ] R−(R+1)sin φ=1 (R+1)cos φ=(√(4R)) P lies on ine through rightmost corner and bisector of angle there. (R+1)sin φ−R ={(R+1)cos φ−Rtan θ}tan ((π/4)−(θ/2)) ⇒ −1=(((2(√R)−Rtan θ)(1−tan θ))/((1+tan θ))) ⇒ 1+tan θ=(tan θ−1))(2(√R)−Rtan θ) ⇒ Rtan^2 θ−(R+2(√R)−1)tan θ +(1+2(√R))=0 tan θ=(((R+2(√R)−1))/(2R))±(√(((R+2(√R)−1)^2 −4R(1+2(√R)))/(4R^2 ))) also tan θ=(√((1/({1−2((a/(R−a)))^2 }^2 ))−1))

$${centre}\:{of}\:{largest}\:\left({here}\right)\:{circle} \\ $$$${be}\:{origin}. \\ $$$${y}={mx}\:\:\:\:{line}\:{eq}.\:\:\:{m}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$${at}\:\:{y}={R},\:\:{x}={R}\mathrm{tan}\:\theta \\ $$$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{a}}{{R}−{a}} \\ $$$$\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{1}}{\left\{\mathrm{1}−\mathrm{2}\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} }−\mathrm{1}} \\ $$$${P}\left[\left({R}+\mathrm{1}\right)\mathrm{cos}\:\phi,\:\left({R}+\mathrm{1}\right)\mathrm{sin}\:\phi\right] \\ $$$${R}−\left({R}+\mathrm{1}\right)\mathrm{sin}\:\phi=\mathrm{1} \\ $$$$\left({R}+\mathrm{1}\right)\mathrm{cos}\:\phi=\sqrt{\mathrm{4}{R}} \\ $$$${P}\:{lies}\:{on}\:{ine}\:{through}\:{rightmost}\: \\ $$$${corner}\:{and}\:{bisector}\:{of}\:{angle}\:{there}. \\ $$$$\left({R}+\mathrm{1}\right)\mathrm{sin}\:\phi−{R} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left\{\left({R}+\mathrm{1}\right)\mathrm{cos}\:\phi−{R}\mathrm{tan}\:\theta\right\}\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow \\ $$$$−\mathrm{1}=\frac{\left(\mathrm{2}\sqrt{{R}}−{R}\mathrm{tan}\:\theta\right)\left(\mathrm{1}−\mathrm{tan}\:\theta\right)}{\left(\mathrm{1}+\mathrm{tan}\:\theta\right)} \\ $$$$\Rightarrow \\ $$$$\left.\:\mathrm{1}+\mathrm{tan}\:\theta=\left(\mathrm{tan}\:\theta−\mathrm{1}\right)\right)\left(\mathrm{2}\sqrt{{R}}−{R}\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow \\ $$$${R}\mathrm{tan}\:^{\mathrm{2}} \theta−\left({R}+\mathrm{2}\sqrt{{R}}−\mathrm{1}\right)\mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{1}+\mathrm{2}\sqrt{{R}}\right)=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta=\frac{\left({R}+\mathrm{2}\sqrt{{R}}−\mathrm{1}\right)}{\mathrm{2}{R}}\pm\sqrt{\frac{\left({R}+\mathrm{2}\sqrt{{R}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{R}\left(\mathrm{1}+\mathrm{2}\sqrt{{R}}\right)}{\mathrm{4}{R}^{\mathrm{2}} }} \\ $$$${also}\:\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{1}}{\left\{\mathrm{1}−\mathrm{2}\left(\frac{{a}}{{R}−{a}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com