
Question Number 204171 by cherokeesay last updated on 07/Feb/24
Commented by deleteduser1 last updated on 07/Feb/24
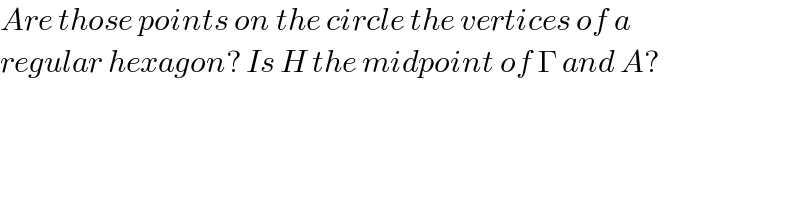
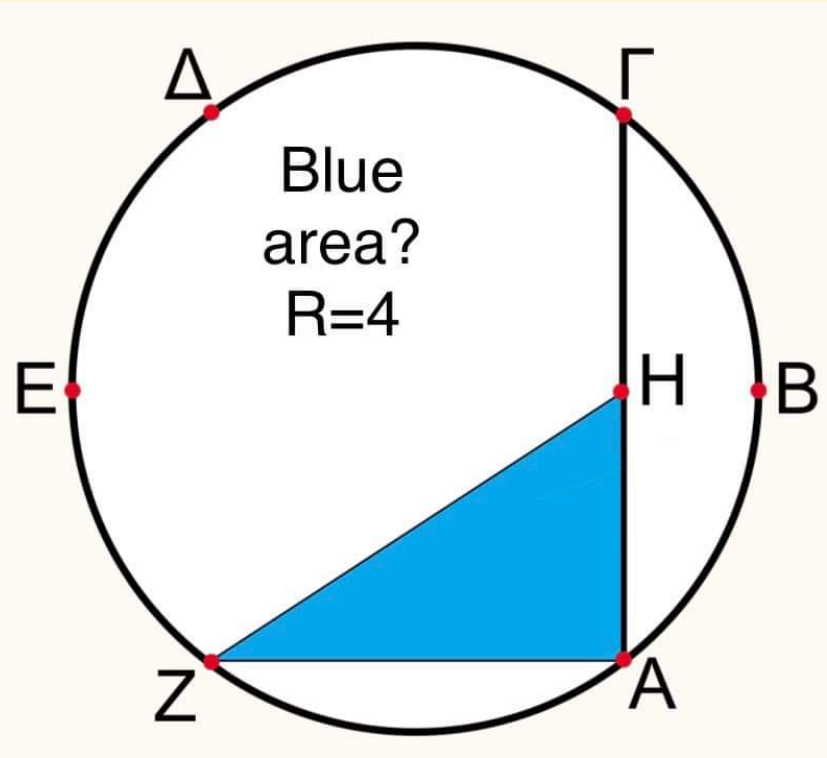
$${Are}\:{those}\:{points}\:{on}\:{the}\:{circle}\:{the}\:{vertices}\:{of}\:{a} \\ $$$${regular}\:{hexagon}?\:{Is}\:{H}\:{the}\:{midpoint}\:{of}\:\Gamma\:{and}\:{A}? \\ $$
Answered by deleteduser1 last updated on 07/Feb/24
![If comment above is true,then ZA=4, ΓA^2 =4^2 +4^2 −2×4^2 cos120=3×4^2 ⇒ΓA=4(√3) ⇒HA=2(√3)⇒[HAZ]=(1/2)×2(√3)×4=4(√3)](Q204173.png)
$${If}\:{comment}\:{above}\:{is}\:{true},{then}\:{ZA}=\mathrm{4}, \\ $$$$\Gamma{A}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} −\mathrm{2}×\mathrm{4}^{\mathrm{2}} {cos}\mathrm{120}=\mathrm{3}×\mathrm{4}^{\mathrm{2}} \Rightarrow\Gamma{A}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{HA}=\mathrm{2}\sqrt{\mathrm{3}}\Rightarrow\left[{HAZ}\right]=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{3}}×\mathrm{4}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$
