Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 204145 by cortano12 last updated on 07/Feb/24

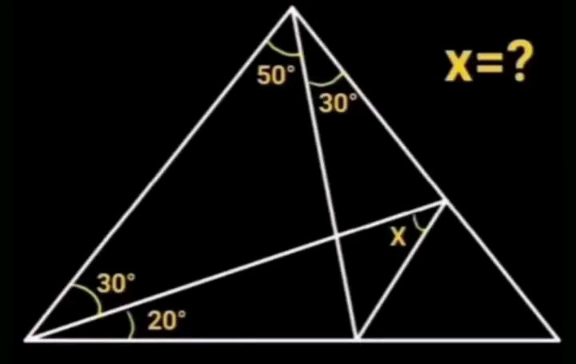
Answered by deleteduser1 last updated on 07/Feb/24

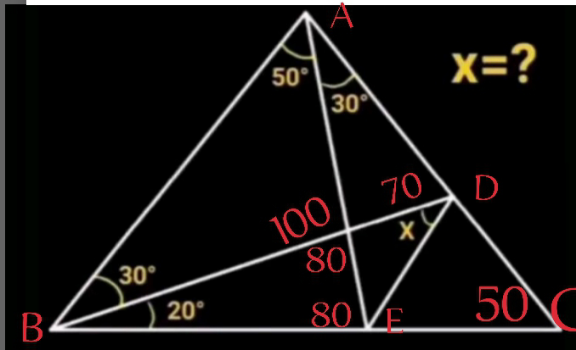
Commented by cortano12 last updated on 08/Feb/24

i got x=40°

$$\:\mathrm{i}\:\mathrm{got}\:\mathrm{x}=\mathrm{40}° \\ $$

Commented by deleteduser1 last updated on 07/Feb/24

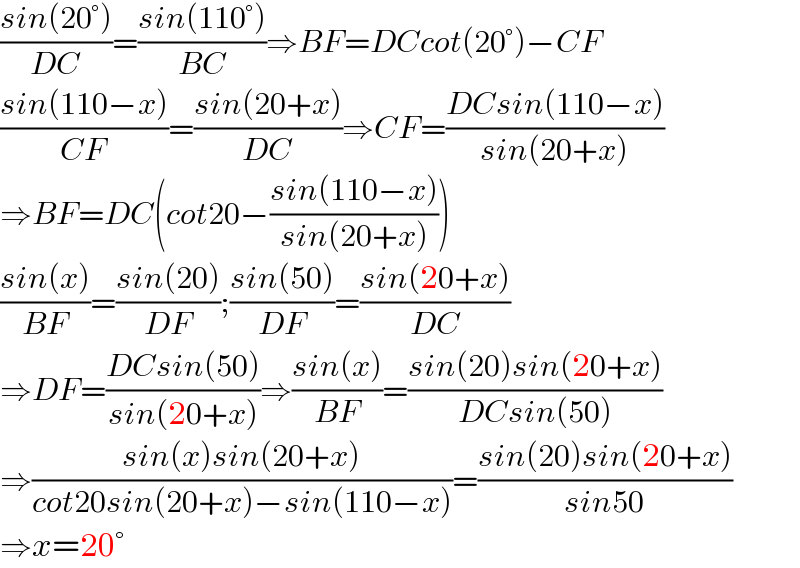
((sin(20°))/(DC))=((sin(110°))/(BC))⇒BF=DCcot(20°)−CF ((sin(110−x))/(CF))=((sin(20+x))/(DC))⇒CF=((DCsin(110−x))/(sin(20+x))) ⇒BF=DC(cot20−((sin(110−x))/(sin(20+x)))) ((sin(x))/(BF))=((sin(20))/(DF));((sin(50))/(DF))=((sin(20+x))/(DC)) ⇒DF=((DCsin(50))/(sin(20+x)))⇒((sin(x))/(BF))=((sin(20)sin(20+x))/(DCsin(50))) ⇒((sin(x)sin(20+x))/(cot20sin(20+x)−sin(110−x)))=((sin(20)sin(20+x))/(sin50)) ⇒x=20°

$$\frac{{sin}\left(\mathrm{20}°\right)}{{DC}}=\frac{{sin}\left(\mathrm{110}°\right)}{{BC}}\Rightarrow{BF}={DCcot}\left(\mathrm{20}°\right)−{CF} \\ $$$$\frac{{sin}\left(\mathrm{110}−{x}\right)}{{CF}}=\frac{{sin}\left(\mathrm{20}+{x}\right)}{{DC}}\Rightarrow{CF}=\frac{{DCsin}\left(\mathrm{110}−{x}\right)}{{sin}\left(\mathrm{20}+{x}\right)} \\ $$$$\Rightarrow{BF}={DC}\left({cot}\mathrm{20}−\frac{{sin}\left(\mathrm{110}−{x}\right)}{{sin}\left(\mathrm{20}+{x}\right)}\right) \\ $$$$\frac{{sin}\left({x}\right)}{{BF}}=\frac{{sin}\left(\mathrm{20}\right)}{{DF}};\frac{{sin}\left(\mathrm{50}\right)}{{DF}}=\frac{{sin}\left(\mathrm{20}+{x}\right)}{{DC}} \\ $$$$\Rightarrow{DF}=\frac{{DCsin}\left(\mathrm{50}\right)}{{sin}\left(\mathrm{20}+{x}\right)}\Rightarrow\frac{{sin}\left({x}\right)}{{BF}}=\frac{{sin}\left(\mathrm{20}\right){sin}\left(\mathrm{20}+{x}\right)}{{DCsin}\left(\mathrm{50}\right)} \\ $$$$\Rightarrow\frac{{sin}\left({x}\right){sin}\left(\mathrm{20}+{x}\right)}{{cot}\mathrm{20}{sin}\left(\mathrm{20}+{x}\right)−{sin}\left(\mathrm{110}−{x}\right)}=\frac{{sin}\left(\mathrm{20}\right){sin}\left(\mathrm{20}+{x}\right)}{{sin}\mathrm{50}} \\ $$$$\Rightarrow{x}=\mathrm{20}° \\ $$

Commented by deleteduser1 last updated on 08/Feb/24

Your solution?

$${Your}\:{solution}? \\ $$

Commented by A5T last updated on 27/Aug/24

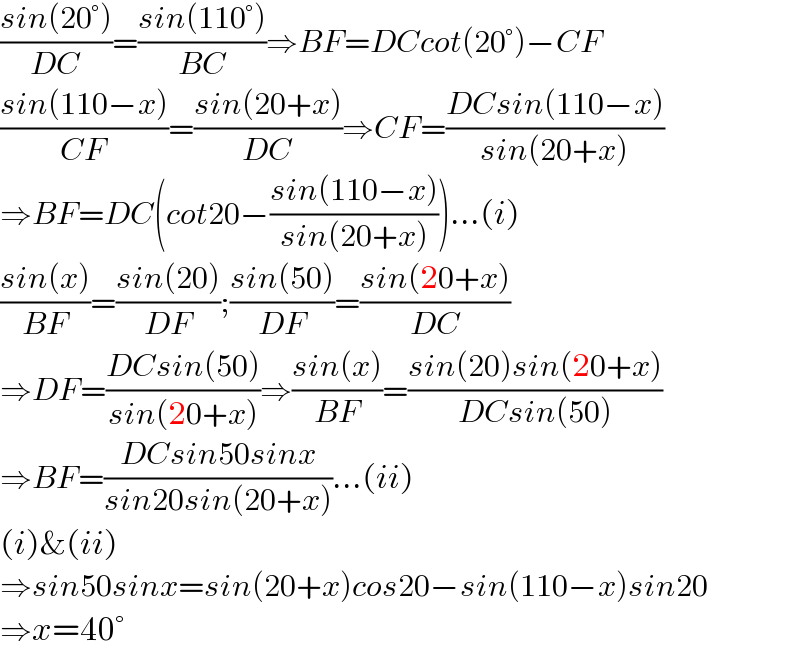
((sin(20°))/(DC))=((sin(110°))/(BC))⇒BF=DCcot(20°)−CF ((sin(110−x))/(CF))=((sin(20+x))/(DC))⇒CF=((DCsin(110−x))/(sin(20+x))) ⇒BF=DC(cot20−((sin(110−x))/(sin(20+x))))...(i) ((sin(x))/(BF))=((sin(20))/(DF));((sin(50))/(DF))=((sin(20+x))/(DC)) ⇒DF=((DCsin(50))/(sin(20+x)))⇒((sin(x))/(BF))=((sin(20)sin(20+x))/(DCsin(50))) ⇒BF=((DCsin50sinx)/(sin20sin(20+x)))...(ii) (i)&(ii) ⇒sin50sinx=sin(20+x)cos20−sin(110−x)sin20 ⇒x=40°

$$\frac{{sin}\left(\mathrm{20}°\right)}{{DC}}=\frac{{sin}\left(\mathrm{110}°\right)}{{BC}}\Rightarrow{BF}={DCcot}\left(\mathrm{20}°\right)−{CF} \\ $$$$\frac{{sin}\left(\mathrm{110}−{x}\right)}{{CF}}=\frac{{sin}\left(\mathrm{20}+{x}\right)}{{DC}}\Rightarrow{CF}=\frac{{DCsin}\left(\mathrm{110}−{x}\right)}{{sin}\left(\mathrm{20}+{x}\right)} \\ $$$$\Rightarrow{BF}={DC}\left({cot}\mathrm{20}−\frac{{sin}\left(\mathrm{110}−{x}\right)}{{sin}\left(\mathrm{20}+{x}\right)}\right)...\left({i}\right) \\ $$$$\frac{{sin}\left({x}\right)}{{BF}}=\frac{{sin}\left(\mathrm{20}\right)}{{DF}};\frac{{sin}\left(\mathrm{50}\right)}{{DF}}=\frac{{sin}\left(\mathrm{20}+{x}\right)}{{DC}} \\ $$$$\Rightarrow{DF}=\frac{{DCsin}\left(\mathrm{50}\right)}{{sin}\left(\mathrm{20}+{x}\right)}\Rightarrow\frac{{sin}\left({x}\right)}{{BF}}=\frac{{sin}\left(\mathrm{20}\right){sin}\left(\mathrm{20}+{x}\right)}{{DCsin}\left(\mathrm{50}\right)} \\ $$$$\Rightarrow{BF}=\frac{{DCsin}\mathrm{50}{sinx}}{{sin}\mathrm{20}{sin}\left(\mathrm{20}+{x}\right)}...\left({ii}\right) \\ $$$$\left({i}\right)\&\left({ii}\right) \\ $$$$\Rightarrow{sin}\mathrm{50}{sinx}={sin}\left(\mathrm{20}+{x}\right){cos}\mathrm{20}−{sin}\left(\mathrm{110}−{x}\right){sin}\mathrm{20} \\ $$$$\Rightarrow{x}=\mathrm{40}° \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com