
Question Number 203891 by York12 last updated on 02/Feb/24

$$ \\ $$
Answered by sniper237 last updated on 01/Feb/24

$${The}\:{last}\:{factor}\:{should}\:{be}\:\left(\frac{{c}}{{a}+{b}}+\frac{{a}}{{b}+{c}}\right) \\ $$$${If}\:\:{so}\:,\:{Let}\:{named}\:{P}\:{that}\:{product} \\ $$$${Divide}\:{each}\:{factor}\:{by}\:{c},{a},{b}\:{resp} \\ $$$${P}=\left(\frac{{a}/{c}}{\mathrm{1}+{b}/{c}}+\frac{{b}/{c}}{\mathrm{1}+{a}/{c}}\right).... \\ $$$${P}\geqslant\left(\frac{{a}+{b}}{{c}}\right)\left(\frac{{b}+{c}}{{a}}\right)\left(\frac{{c}+{a}}{{b}}\right)\geqslant\frac{\mathrm{2}\sqrt{{ab}}\mathrm{2}\sqrt{{bc}}\mathrm{2}\sqrt{{ca}}}{{abc}} \\ $$$${Then}\:{P}\geqslant\mathrm{8} \\ $$
Commented by York12 last updated on 02/Feb/24

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by York12 last updated on 02/Feb/24

Commented by York12 last updated on 02/Feb/24
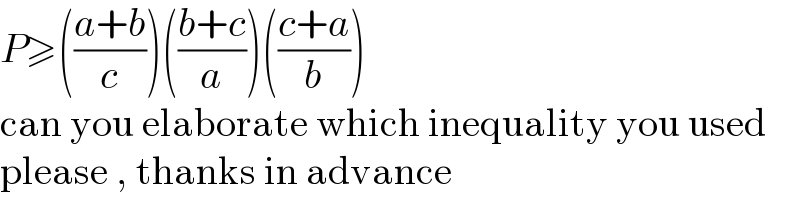
$${P}\geqslant\left(\frac{{a}+{b}}{{c}}\right)\left(\frac{{b}+{c}}{{a}}\right)\left(\frac{{c}+{a}}{{b}}\right) \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{elaborate}\:\mathrm{which}\:\mathrm{inequality}\:\mathrm{you}\:\mathrm{used} \\ $$$$\mathrm{please}\:,\:\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance} \\ $$
