Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 203771 by Calculusboy last updated on 27/Jan/24

Answered by DwaipayanShikari last updated on 27/Jan/24

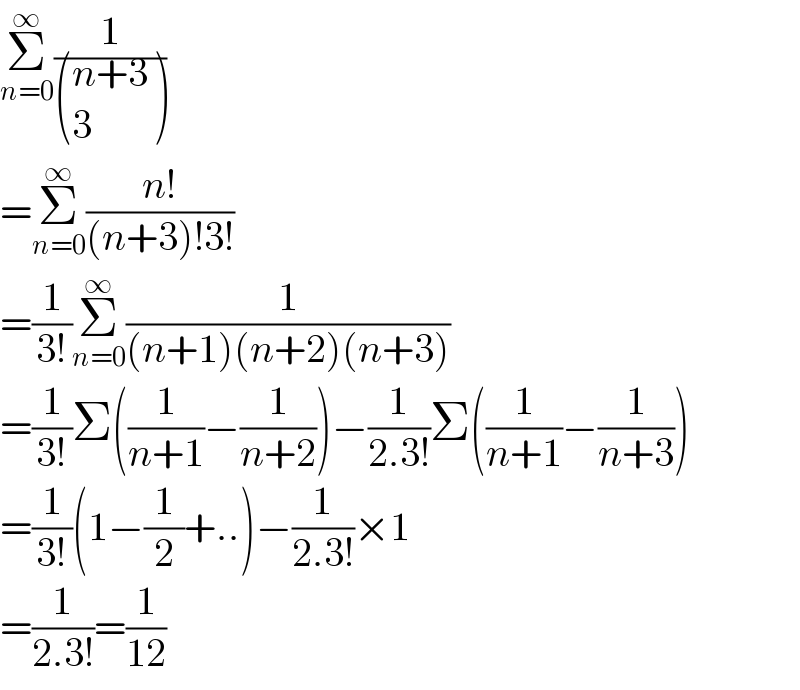
Σ_(n=0) ^∞ (1/ (((n+3)),(3) )) =Σ_(n=0) ^∞ ((n!)/((n+3)!3!)) =(1/(3!))Σ_(n=0) ^∞ (1/((n+1)(n+2)(n+3))) =(1/(3!))Σ((1/(n+1))−(1/(n+2)))−(1/(2.3!))Σ((1/(n+1))−(1/(n+3))) =(1/(3!))(1−(1/2)+..)−(1/(2.3!))×1 =(1/(2.3!))=(1/(12))

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\begin{pmatrix}{{n}+\mathrm{3}}\\{\mathrm{3}}\end{pmatrix}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}!}{\left({n}+\mathrm{3}\right)!\mathrm{3}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}!}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}!}\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}!}\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}!}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+..\right)−\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}!}×\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}!}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$

Commented by aleks041103 last updated on 31/Jan/24

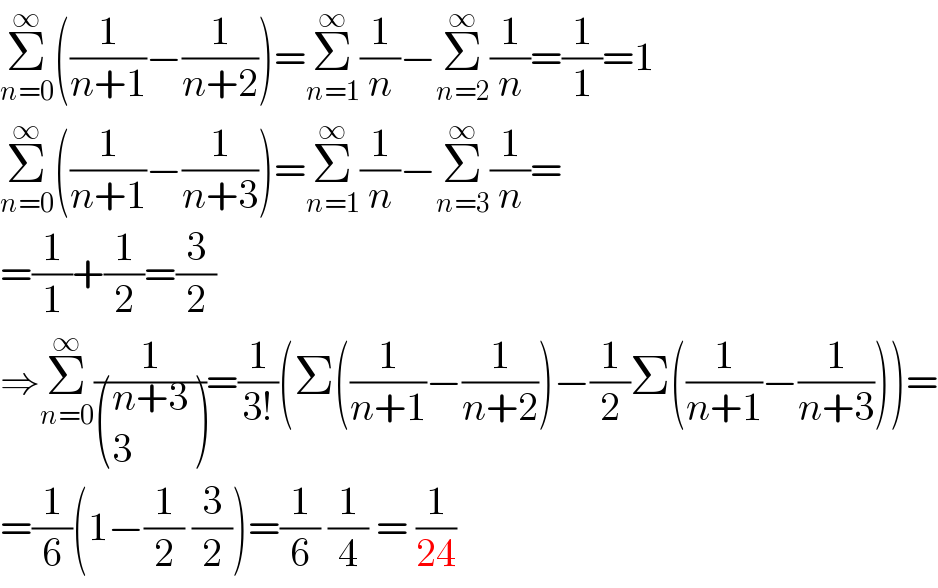
Σ_(n=0) ^∞ ((1/(n+1))−(1/(n+2)))=Σ_(n=1) ^∞ (1/n)−Σ_(n=2) ^∞ (1/n)=(1/1)=1 Σ_(n=0) ^∞ ((1/(n+1))−(1/(n+3)))=Σ_(n=1) ^∞ (1/n)−Σ_(n=3) ^∞ (1/n)= =(1/1)+(1/2)=(3/2) ⇒Σ_(n=0) ^∞ (1/ (((n+3)),(3) ))=(1/(3!))(Σ((1/(n+1))−(1/(n+2)))−(1/2)Σ((1/(n+1))−(1/(n+3))))= =(1/6)(1−(1/2) (3/2))=(1/6) (1/4) = (1/(24))

$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\begin{pmatrix}{{n}+\mathrm{3}}\\{\mathrm{3}}\end{pmatrix}}=\frac{\mathrm{1}}{\mathrm{3}!}\left(\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{6}}\:\frac{\mathrm{1}}{\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{24}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com