Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 203742 by Calculusboy last updated on 27/Jan/24

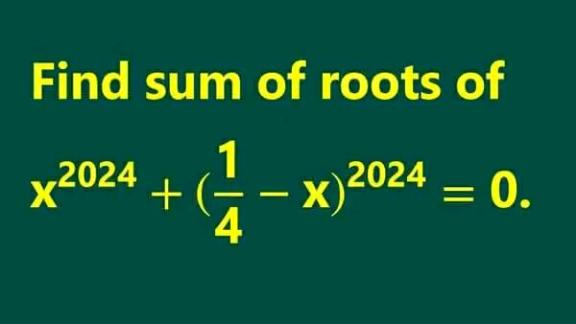
Answered by mr W last updated on 27/Jan/24

x^(2024) +x^(2024) −2024×(1/4)x^(2023) +...=0 2x^(2024) −506x^(2023) +...=0 sum of roots =((506)/2)=253 ✓ solution: ((1/(4x))−1)^(2024) =−1=e^((2k+1)πi) (1/(4x))−1=e^(((2k+1)πi)/(2024)) ⇒x=(1/(4[1+e^(((2k+1)πi)/(2024)) ])) with k=0,1,...,2023

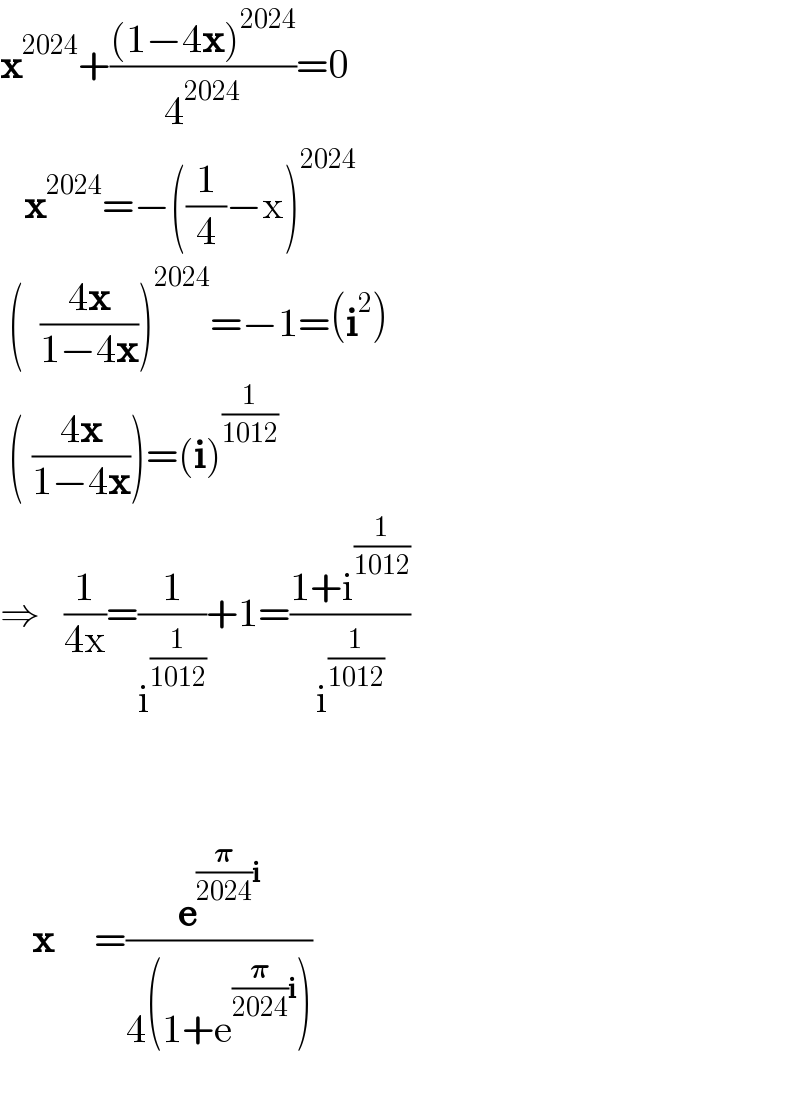
$${x}^{\mathrm{2024}} +{x}^{\mathrm{2024}} −\mathrm{2024}×\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2023}} +...=\mathrm{0} \\ $$$$\mathrm{2}{x}^{\mathrm{2024}} −\mathrm{506}{x}^{\mathrm{2023}} +...=\mathrm{0} \\ $$$${sum}\:{of}\:{roots}\:=\frac{\mathrm{506}}{\mathrm{2}}=\mathrm{253}\:\checkmark \\ $$$$ \\ $$$${solution}: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{4}{x}}−\mathrm{1}\right)^{\mathrm{2024}} =−\mathrm{1}={e}^{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{x}}−\mathrm{1}={e}^{\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}}{\mathrm{2024}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{4}\left[\mathrm{1}+{e}^{\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi{i}}{\mathrm{2024}}} \right]}\:\:{with}\:{k}=\mathrm{0},\mathrm{1},...,\mathrm{2023} \\ $$

Commented by Calculusboy last updated on 27/Jan/24

thanks sir

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$

Answered by a.lgnaoui last updated on 27/Jan/24

x^(2024) +(((1−4x)^(2024) )/4^(2024) )=0 x^(2024) =−((1/4)−x)^(2024) ( ((4x)/(1−4x)))^(2024) =−1=(i^2 ) ( ((4x)/(1−4x)))=(i)^(1/(1012)) ⇒ (1/(4x))=(1/i^(1/(1012)) )+1=((1+i^(1/(1012)) )/i^(1/(1012)) ) x =(e^((𝛑/(2024))i) /(4(1+e^((𝛑/(2024))i) )))

$$\boldsymbol{\mathrm{x}}^{\mathrm{2024}} +\frac{\left(\mathrm{1}−\mathrm{4}\boldsymbol{\mathrm{x}}\right)^{\mathrm{2024}} }{\mathrm{4}^{\mathrm{2024}} }=\mathrm{0} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2024}} =−\left(\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{x}\right)^{\mathrm{2024}} \\ $$$$\:\left(\:\:\frac{\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{1}−\mathrm{4}\boldsymbol{\mathrm{x}}}\right)^{\mathrm{2024}} =−\mathrm{1}=\left(\boldsymbol{\mathrm{i}}^{\mathrm{2}} \right) \\ $$$$\:\left(\:\frac{\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{1}−\mathrm{4}\boldsymbol{\mathrm{x}}}\right)=\left(\boldsymbol{\mathrm{i}}\right)^{\frac{\mathrm{1}}{\mathrm{1012}}} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{1}}{\mathrm{4x}}=\frac{\mathrm{1}}{\mathrm{i}^{\frac{\mathrm{1}}{\mathrm{1012}}} }+\mathrm{1}=\frac{\mathrm{1}+\mathrm{i}^{\frac{\mathrm{1}}{\mathrm{1012}}} }{\mathrm{i}^{\frac{\mathrm{1}}{\mathrm{1012}}} } \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}\:\:\:\:\:=\frac{\boldsymbol{\mathrm{e}}^{\frac{\boldsymbol{\pi}}{\mathrm{2024}}\boldsymbol{\mathrm{i}}} }{\mathrm{4}\left(\mathrm{1}+\mathrm{e}^{\frac{\boldsymbol{\pi}}{\mathrm{2024}}\boldsymbol{\mathrm{i}}} \right)} \\ $$$$\:\:\:\:\:\:\:\: \\ $$

Commented by mr W last updated on 27/Jan/24

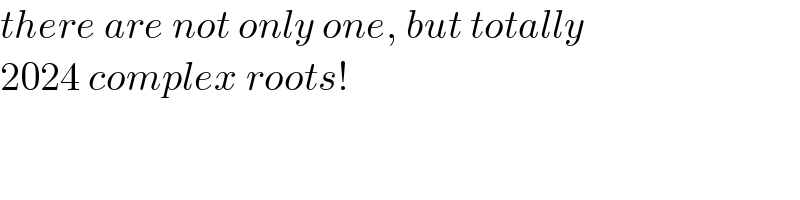
there are not only one, but totally 2024 complex roots!

$${there}\:{are}\:{not}\:{only}\:{one},\:{but}\:{totally} \\ $$$$\mathrm{2024}\:{complex}\:{roots}! \\ $$

Commented by Calculusboy last updated on 27/Jan/24

thanks sir

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$

Commented by a.lgnaoui last updated on 27/Jan/24

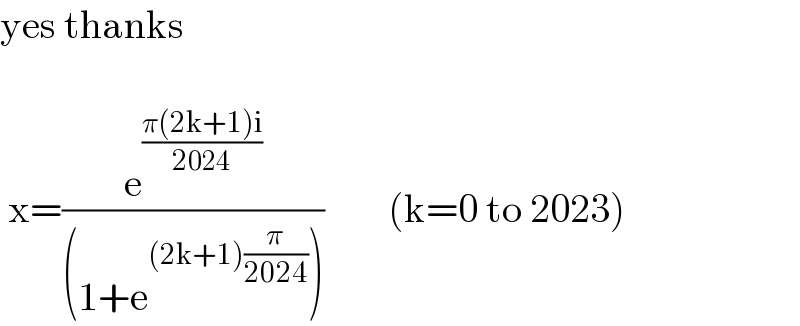
yes thanks x=(e^((π(2k+1)i)/(2024)) /((1+e^((2k+1)(π/(2024))) ))) (k=0 to 2023)

$$\mathrm{yes}\:\mathrm{thanks}\: \\ $$$$ \\ $$$$\:\mathrm{x}=\frac{\mathrm{e}^{\frac{\pi\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}}{\mathrm{2024}}} }{\left(\mathrm{1}+\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\frac{\pi}{\mathrm{2024}}} \right)}\:\:\:\:\:\:\:\:\left(\mathrm{k}=\mathrm{0}\:\mathrm{to}\:\mathrm{2023}\right) \\ $$

Answered by MathematicalUser2357 last updated on 28/Jan/24

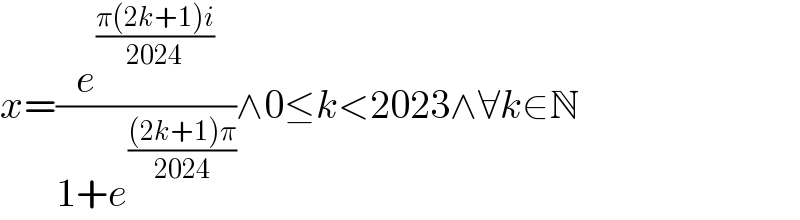
x=(e^((π(2k+1)i)/(2024)) /(1+e^(((2k+1)π)/(2024)) ))∧0≤k<2023∧∀k∈N

$${x}=\frac{{e}^{\frac{\pi\left(\mathrm{2}{k}+\mathrm{1}\right){i}}{\mathrm{2024}}} }{\mathrm{1}+{e}^{\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2024}}} }\wedge\mathrm{0}\leq{k}<\mathrm{2023}\wedge\forall{k}\in\mathbb{N} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com