
Question Number 203625 by professorleiciano last updated on 23/Jan/24

Answered by esmaeil last updated on 23/Jan/24
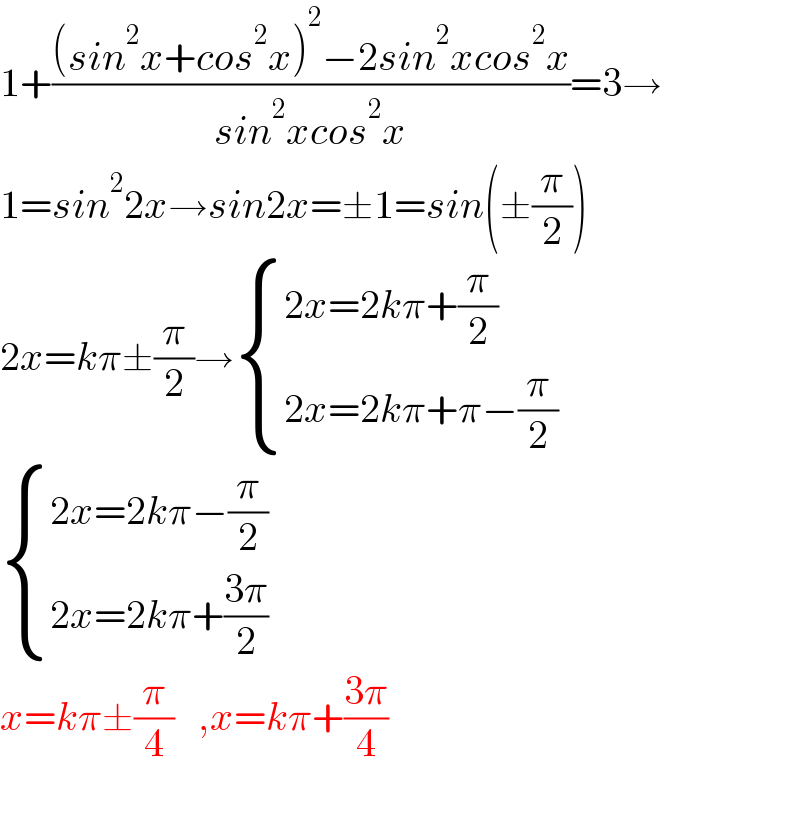
$$\mathrm{1}+\frac{\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}=\mathrm{3}\rightarrow \\ $$$$\mathrm{1}={sin}^{\mathrm{2}} \mathrm{2}{x}\rightarrow{sin}\mathrm{2}{x}=\pm\mathrm{1}={sin}\left(\pm\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{x}={k}\pi\pm\frac{\pi}{\mathrm{2}}\rightarrow\begin{cases}{\mathrm{2}{x}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}}}\\{\mathrm{2}{x}=\mathrm{2}{k}\pi+\pi−\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$$\begin{cases}{\mathrm{2}{x}=\mathrm{2}{k}\pi−\frac{\pi}{\mathrm{2}}}\\{\mathrm{2}{x}=\mathrm{2}{k}\pi+\frac{\mathrm{3}\pi}{\mathrm{2}}}\end{cases} \\ $$$${x}={k}\pi\pm\frac{\pi}{\mathrm{4}}\:\:\:,{x}={k}\pi+\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$ \\ $$
Commented by professorleiciano last updated on 24/Jan/24
Sua resposta está totalmente errada.
Answered by professorleiciano last updated on 23/Jan/24

Commented by esmaeil last updated on 23/Jan/24
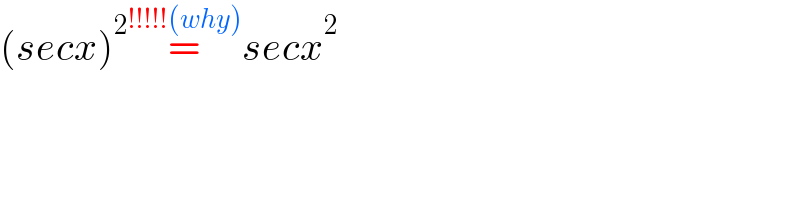
$$\left({secx}\right)^{\mathrm{2}} \overset{!!!!!\left({why}\right)} {=}{secx}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by esmaeil last updated on 24/Jan/24

$${why}\:{do}\:{you}\:{only}\:{answer}\:{your}\:{own} \\ $$$${question}.{your}\:{answer}\:{is}\:{also}\:{wrong}. \\ $$
