
Question Number 203387 by Noorzai last updated on 18/Jan/24
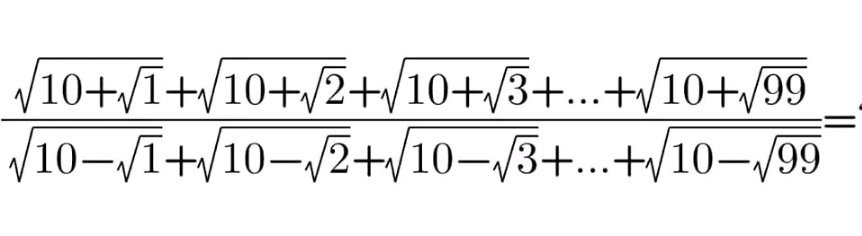
Answered by mr W last updated on 18/Jan/24
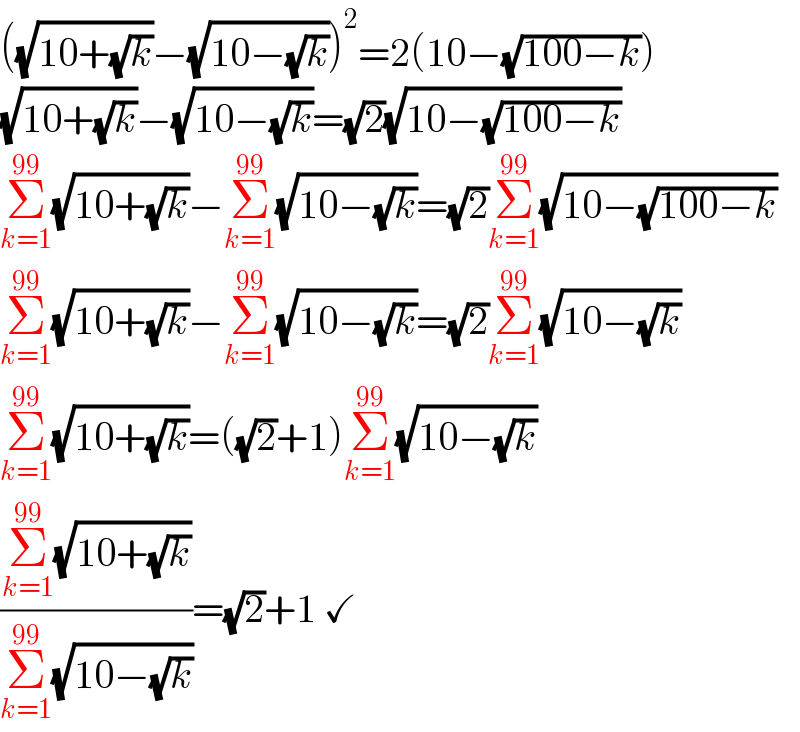
$$\left(\sqrt{\mathrm{10}+\sqrt{{k}}}−\sqrt{\mathrm{10}−\sqrt{{k}}}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{10}−\sqrt{\mathrm{100}−{k}}\right) \\ $$$$\sqrt{\mathrm{10}+\sqrt{{k}}}−\sqrt{\mathrm{10}−\sqrt{{k}}}=\sqrt{\mathrm{2}}\sqrt{\mathrm{10}−\sqrt{\mathrm{100}−{k}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}+\sqrt{{k}}}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{{k}}}=\sqrt{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{\mathrm{100}−{k}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}+\sqrt{{k}}}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{{k}}}=\sqrt{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{{k}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}+\sqrt{{k}}}=\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{{k}}} \\ $$$$\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}+\sqrt{{k}}}}{\underset{{k}=\mathrm{1}} {\overset{\mathrm{99}} {\sum}}\sqrt{\mathrm{10}−\sqrt{{k}}}}=\sqrt{\mathrm{2}}+\mathrm{1}\:\checkmark \\ $$
