Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 203187 by Amidip last updated on 12/Jan/24

Answered by mr W last updated on 12/Jan/24

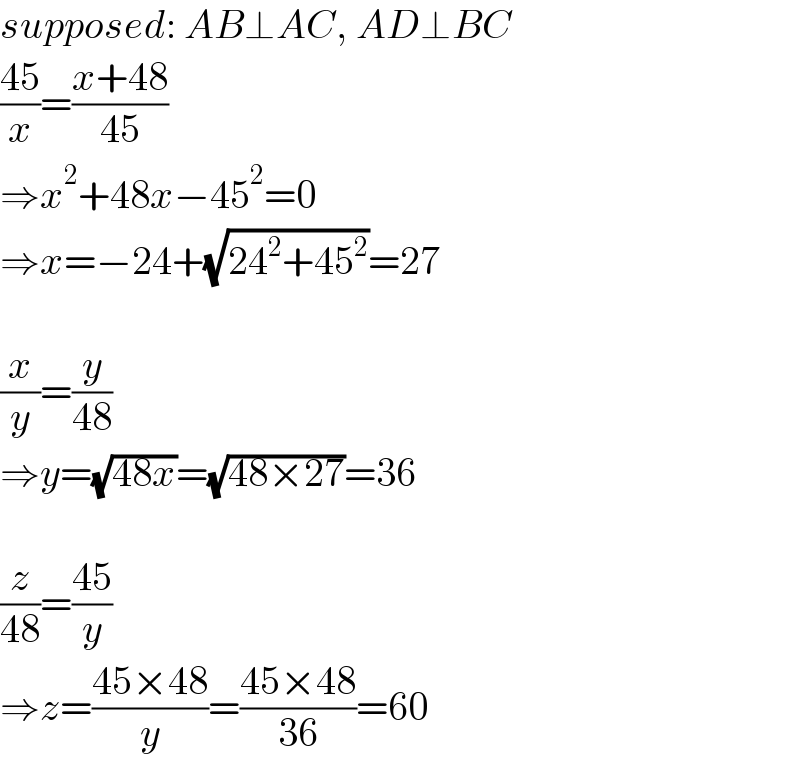
supposed: AB⊥AC, AD⊥BC ((45)/x)=((x+48)/(45)) ⇒x^2 +48x−45^2 =0 ⇒x=−24+(√(24^2 +45^2 ))=27 (x/y)=(y/(48)) ⇒y=(√(48x))=(√(48×27))=36 (z/(48))=((45)/y) ⇒z=((45×48)/y)=((45×48)/(36))=60

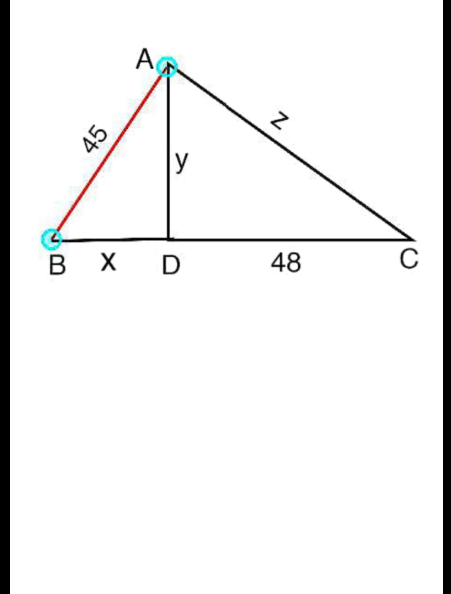
$${supposed}:\:{AB}\bot{AC},\:{AD}\bot{BC} \\ $$$$\frac{\mathrm{45}}{{x}}=\frac{{x}+\mathrm{48}}{\mathrm{45}}\: \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{48}{x}−\mathrm{45}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{24}+\sqrt{\mathrm{24}^{\mathrm{2}} +\mathrm{45}^{\mathrm{2}} }=\mathrm{27} \\ $$$$ \\ $$$$\frac{{x}}{{y}}=\frac{{y}}{\mathrm{48}}\: \\ $$$$\Rightarrow{y}=\sqrt{\mathrm{48}{x}}=\sqrt{\mathrm{48}×\mathrm{27}}=\mathrm{36} \\ $$$$ \\ $$$$\frac{{z}}{\mathrm{48}}=\frac{\mathrm{45}}{{y}} \\ $$$$\Rightarrow{z}=\frac{\mathrm{45}×\mathrm{48}}{{y}}=\frac{\mathrm{45}×\mathrm{48}}{\mathrm{36}}=\mathrm{60} \\ $$

Answered by Rasheed.Sindhi last updated on 12/Jan/24

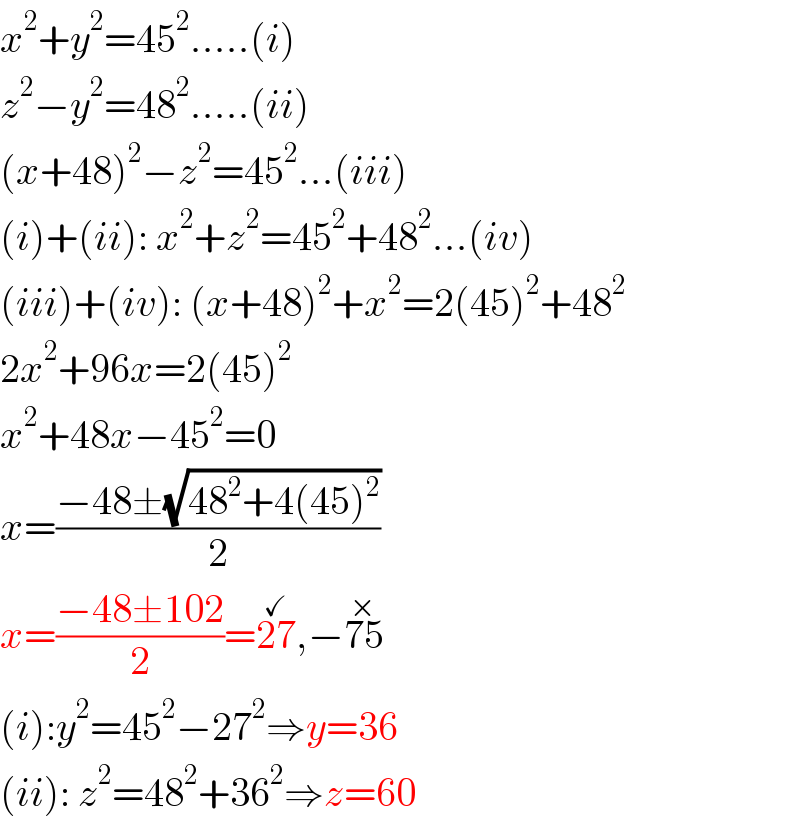
x^2 +y^2 =45^2 .....(i) z^2 −y^2 =48^2 .....(ii) (x+48)^2 −z^2 =45^2 ...(iii) (i)+(ii): x^2 +z^2 =45^2 +48^2 ...(iv) (iii)+(iv): (x+48)^2 +x^2 =2(45)^2 +48^2 2x^2 +96x=2(45)^2 x^2 +48x−45^2 =0 x=((−48±(√(48^2 +4(45)^2 )))/2) x=((−48±102)/2)=27^(✓) ,−75^(×) (i):y^2 =45^2 −27^2 ⇒y=36 (ii): z^2 =48^2 +36^2 ⇒z=60

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{45}^{\mathrm{2}} .....\left({i}\right) \\ $$$${z}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{48}^{\mathrm{2}} .....\left({ii}\right) \\ $$$$\left({x}+\mathrm{48}\right)^{\mathrm{2}} −{z}^{\mathrm{2}} =\mathrm{45}^{\mathrm{2}} ...\left({iii}\right) \\ $$$$\left({i}\right)+\left({ii}\right):\:{x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{45}^{\mathrm{2}} +\mathrm{48}^{\mathrm{2}} ...\left({iv}\right) \\ $$$$\left({iii}\right)+\left({iv}\right):\:\left({x}+\mathrm{48}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{45}\right)^{\mathrm{2}} +\mathrm{48}^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\mathrm{96}{x}=\mathrm{2}\left(\mathrm{45}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{48}{x}−\mathrm{45}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{−\mathrm{48}\pm\sqrt{\mathrm{48}^{\mathrm{2}} +\mathrm{4}\left(\mathrm{45}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{48}\pm\mathrm{102}}{\mathrm{2}}=\overset{\checkmark} {\mathrm{27}},−\overset{×} {\mathrm{75}} \\ $$$$\left({i}\right):{y}^{\mathrm{2}} =\mathrm{45}^{\mathrm{2}} −\mathrm{27}^{\mathrm{2}} \Rightarrow{y}=\mathrm{36} \\ $$$$\left({ii}\right):\:{z}^{\mathrm{2}} =\mathrm{48}^{\mathrm{2}} +\mathrm{36}^{\mathrm{2}} \Rightarrow{z}=\mathrm{60} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com