
Question Number 203180 by Calculusboy last updated on 11/Jan/24
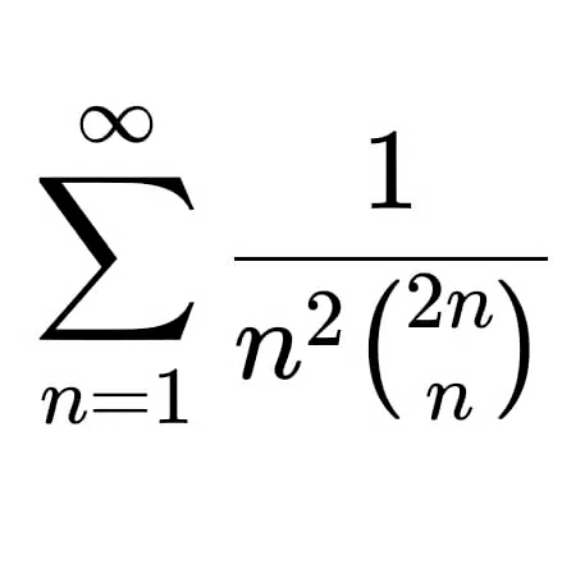
Answered by Rana_Ranino last updated on 11/Jan/24
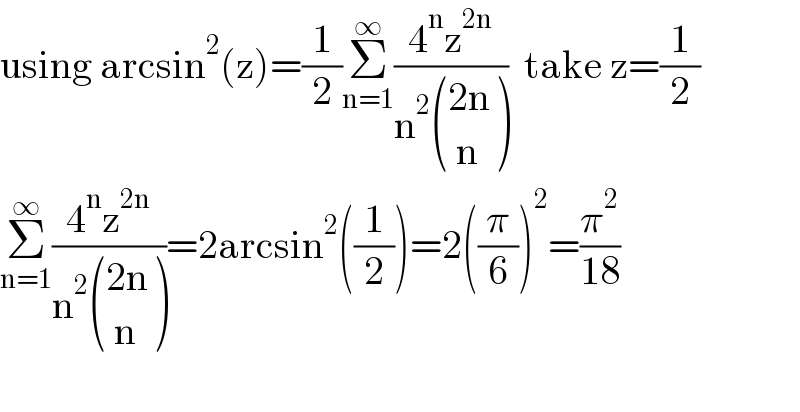
$$\mathrm{using}\:\mathrm{arcsin}^{\mathrm{2}} \left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{\mathrm{n}} \mathrm{z}^{\mathrm{2n}} }{\mathrm{n}^{\mathrm{2}} \begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{n}}\end{pmatrix}}\:\:\mathrm{take}\:\mathrm{z}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{\mathrm{n}} \mathrm{z}^{\mathrm{2n}} }{\mathrm{n}^{\mathrm{2}} \begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{n}}\end{pmatrix}}=\mathrm{2arcsin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{18}} \\ $$$$ \\ $$
Commented by Calculusboy last updated on 11/Jan/24

$$\boldsymbol{{thanks}}\:\boldsymbol{{ma}} \\ $$
