
Question Number 203107 by cherokeesay last updated on 10/Jan/24
Commented by cherokeesay last updated on 10/Jan/24

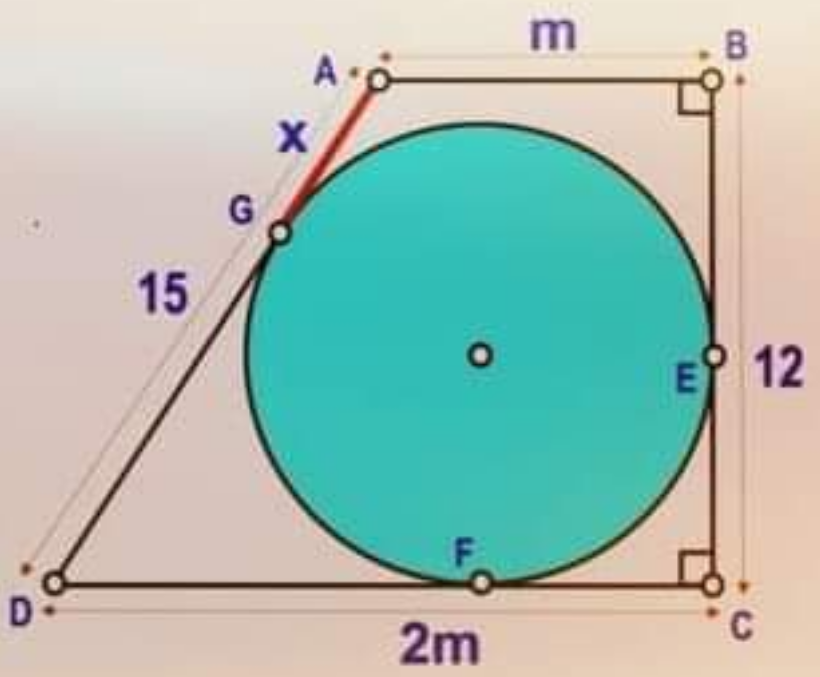
Find the length x.
Answered by deleteduser1 last updated on 10/Jan/24
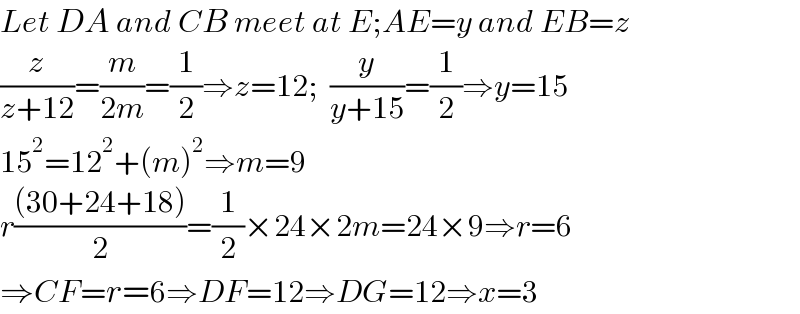
$${Let}\:{DA}\:{and}\:{CB}\:{meet}\:{at}\:{E};{AE}={y}\:{and}\:{EB}={z} \\ $$$$\frac{{z}}{{z}+\mathrm{12}}=\frac{{m}}{\mathrm{2}{m}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{z}=\mathrm{12};\:\:\frac{{y}}{{y}+\mathrm{15}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{y}=\mathrm{15} \\ $$$$\mathrm{15}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} +\left({m}\right)^{\mathrm{2}} \Rightarrow{m}=\mathrm{9} \\ $$$${r}\frac{\left(\mathrm{30}+\mathrm{24}+\mathrm{18}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{24}×\mathrm{2}{m}=\mathrm{24}×\mathrm{9}\Rightarrow{r}=\mathrm{6} \\ $$$$\Rightarrow{CF}={r}=\mathrm{6}\Rightarrow{DF}=\mathrm{12}\Rightarrow{DG}=\mathrm{12}\Rightarrow{x}=\mathrm{3} \\ $$
Commented by cherokeesay last updated on 10/Jan/24

$${So}\:{nice}\:!\:{thank}\:{you}\:! \\ $$
