
Question Number 202765 by Mastermind last updated on 02/Jan/24
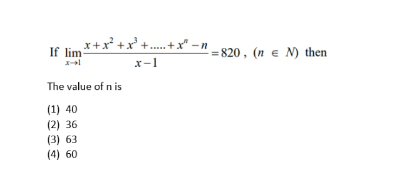
Answered by aleks041103 last updated on 02/Jan/24
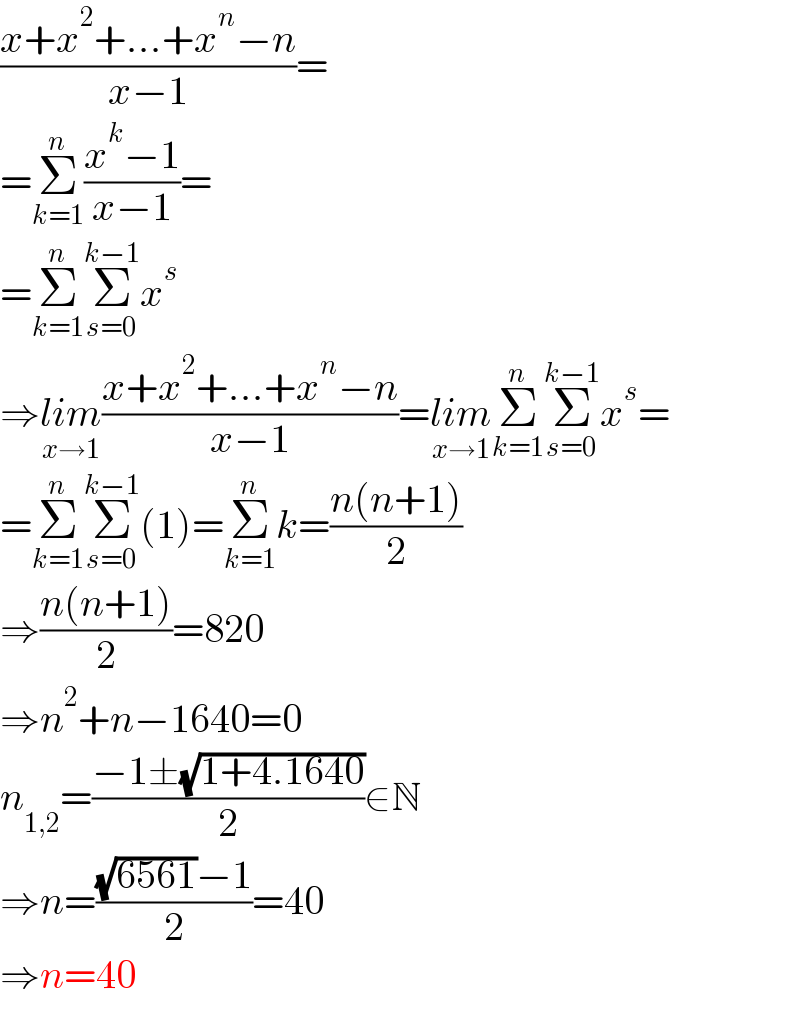
$$\frac{{x}+{x}^{\mathrm{2}} +...+{x}^{{n}} −{n}}{{x}−\mathrm{1}}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{x}^{{k}} −\mathrm{1}}{{x}−\mathrm{1}}= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{s}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}{x}^{{s}} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{{x}+{x}^{\mathrm{2}} +...+{x}^{{n}} −{n}}{{x}−\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{s}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}{x}^{{s}} = \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{{s}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}\left(\mathrm{1}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{820} \\ $$$$\Rightarrow{n}^{\mathrm{2}} +{n}−\mathrm{1640}=\mathrm{0} \\ $$$${n}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}.\mathrm{1640}}}{\mathrm{2}}\in\mathbb{N} \\ $$$$\Rightarrow{n}=\frac{\sqrt{\mathrm{6561}}−\mathrm{1}}{\mathrm{2}}=\mathrm{40} \\ $$$$\Rightarrow{n}=\mathrm{40} \\ $$
Answered by manxsol last updated on 02/Jan/24
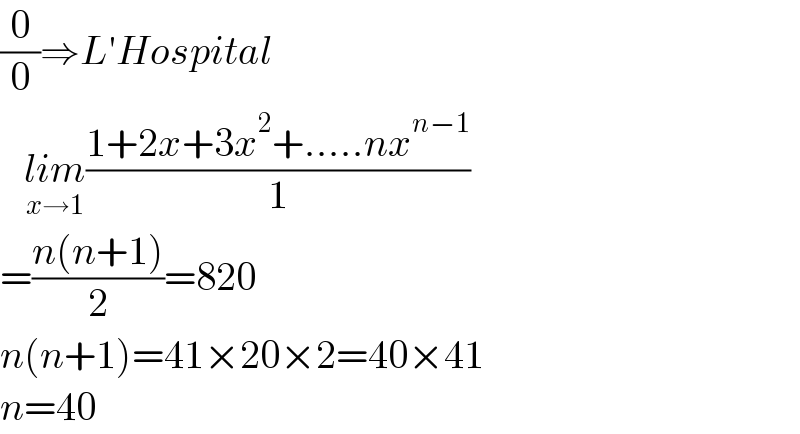
$$\frac{\mathrm{0}}{\mathrm{0}}\Rightarrow{L}'{Hospital} \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{1}} {{lim}}\frac{\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +.....{nx}^{{n}−\mathrm{1}} }{\mathrm{1}} \\ $$$$=\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{820} \\ $$$${n}\left({n}+\mathrm{1}\right)=\mathrm{41}×\mathrm{20}×\mathrm{2}=\mathrm{40}×\mathrm{41} \\ $$$${n}=\mathrm{40} \\ $$
