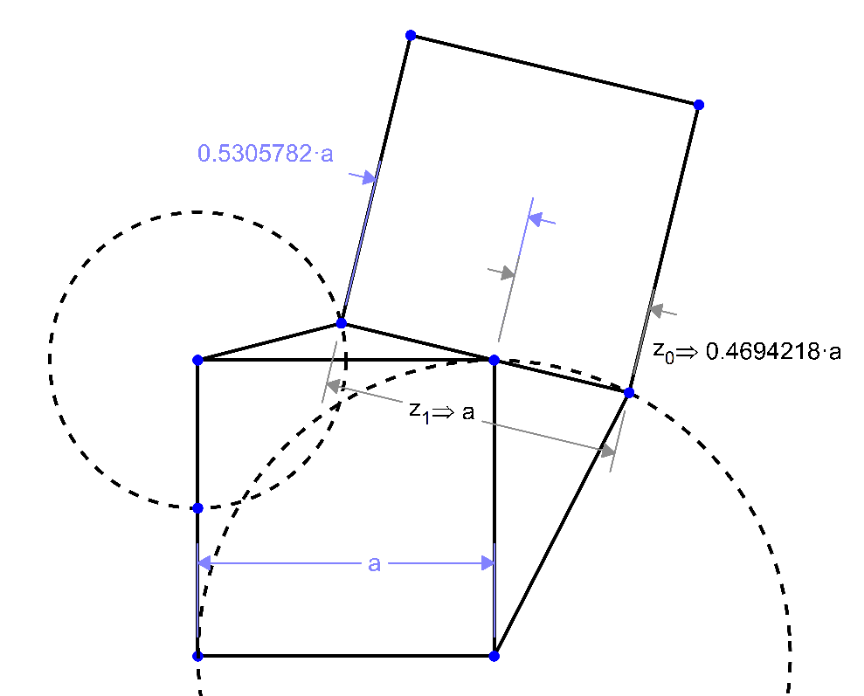
Question Number 202684 by ajfour last updated on 31/Dec/23
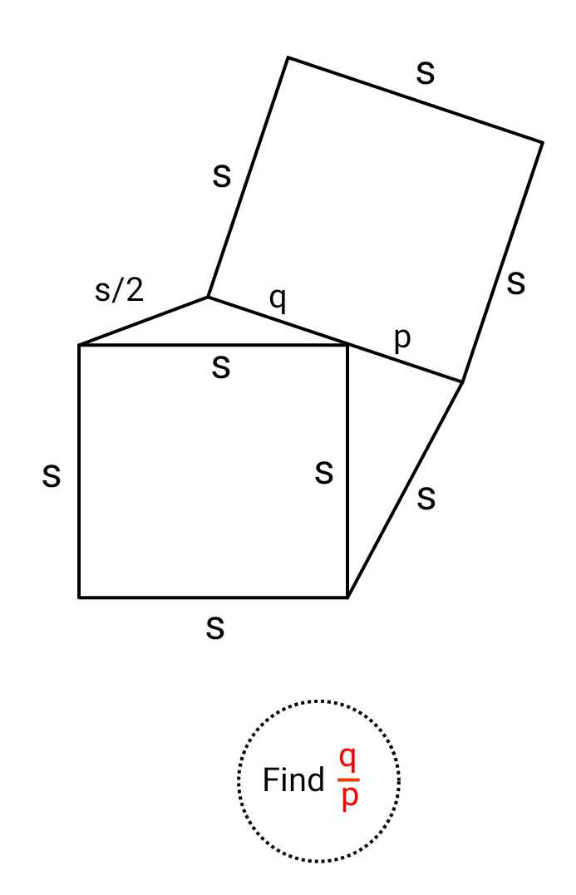
Answered by mr W last updated on 02/Jan/24
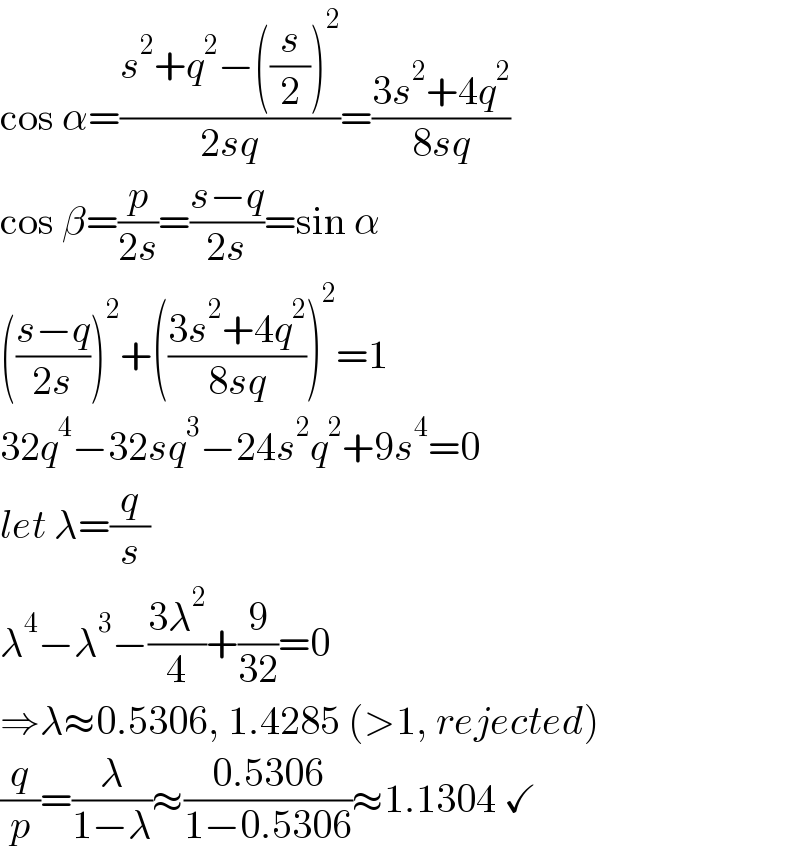
$$\mathrm{cos}\:\alpha=\frac{{s}^{\mathrm{2}} +{q}^{\mathrm{2}} −\left(\frac{{s}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}{sq}}=\frac{\mathrm{3}{s}^{\mathrm{2}} +\mathrm{4}{q}^{\mathrm{2}} }{\mathrm{8}{sq}} \\ $$$$\mathrm{cos}\:\beta=\frac{{p}}{\mathrm{2}{s}}=\frac{{s}−{q}}{\mathrm{2}{s}}=\mathrm{sin}\:\alpha \\ $$$$\left(\frac{{s}−{q}}{\mathrm{2}{s}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}{s}^{\mathrm{2}} +\mathrm{4}{q}^{\mathrm{2}} }{\mathrm{8}{sq}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{32}{q}^{\mathrm{4}} −\mathrm{32}{sq}^{\mathrm{3}} −\mathrm{24}{s}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{9}{s}^{\mathrm{4}} =\mathrm{0} \\ $$$${let}\:\lambda=\frac{{q}}{{s}} \\ $$$$\lambda^{\mathrm{4}} −\lambda^{\mathrm{3}} −\frac{\mathrm{3}\lambda^{\mathrm{2}} }{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{32}}=\mathrm{0} \\ $$$$\Rightarrow\lambda\approx\mathrm{0}.\mathrm{5306},\:\mathrm{1}.\mathrm{4285}\:\left(>\mathrm{1},\:{rejected}\right) \\ $$$$\frac{{q}}{{p}}=\frac{\lambda}{\mathrm{1}−\lambda}\approx\frac{\mathrm{0}.\mathrm{5306}}{\mathrm{1}−\mathrm{0}.\mathrm{5306}}\approx\mathrm{1}.\mathrm{1304}\:\checkmark \\ $$
Commented by mr W last updated on 01/Jan/24
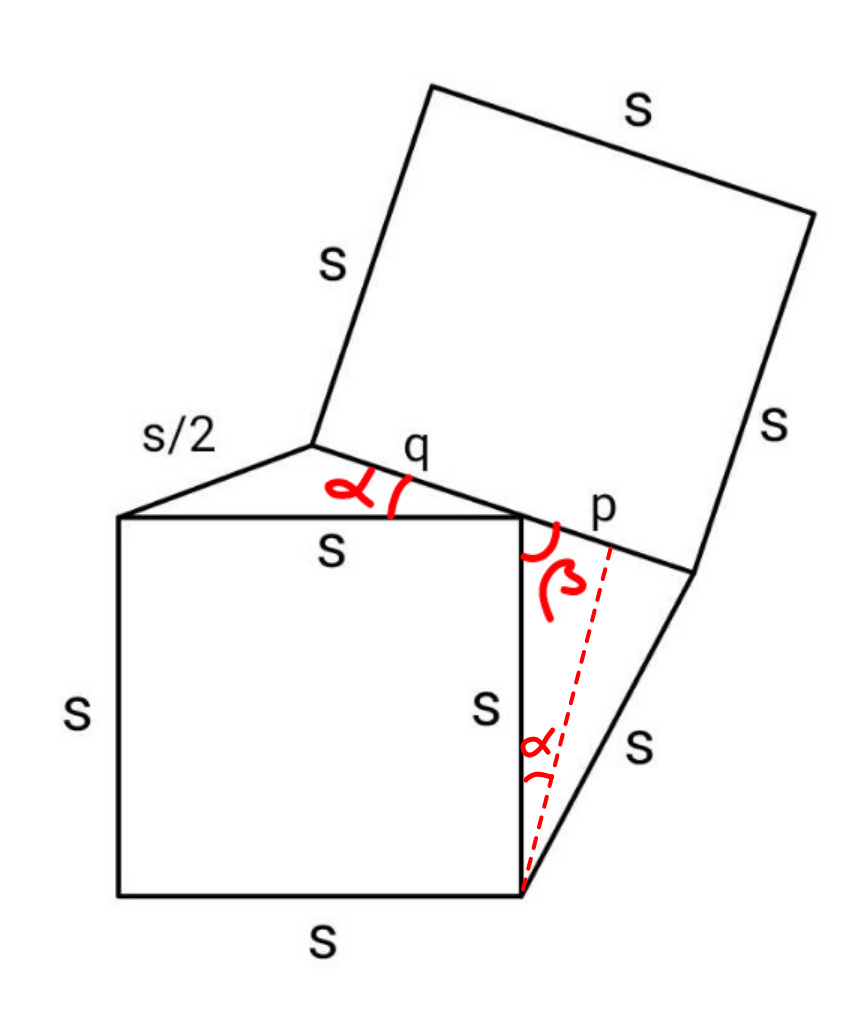
Commented by ajfour last updated on 01/Jan/24

$${Thanks}\:{Sir}!\:{I}\:{have}\:{attached}\:{an} \\ $$$${image}\:{corresponding}\:{to}\:{your}\: \\ $$$${answer},\:{than}\:{mine}! \\ $$
Commented by mr W last updated on 01/Jan/24