
Question Number 202591 by Calculusboy last updated on 30/Dec/23
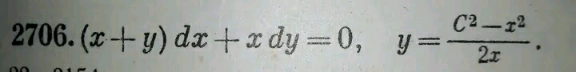
Answered by mr W last updated on 30/Dec/23
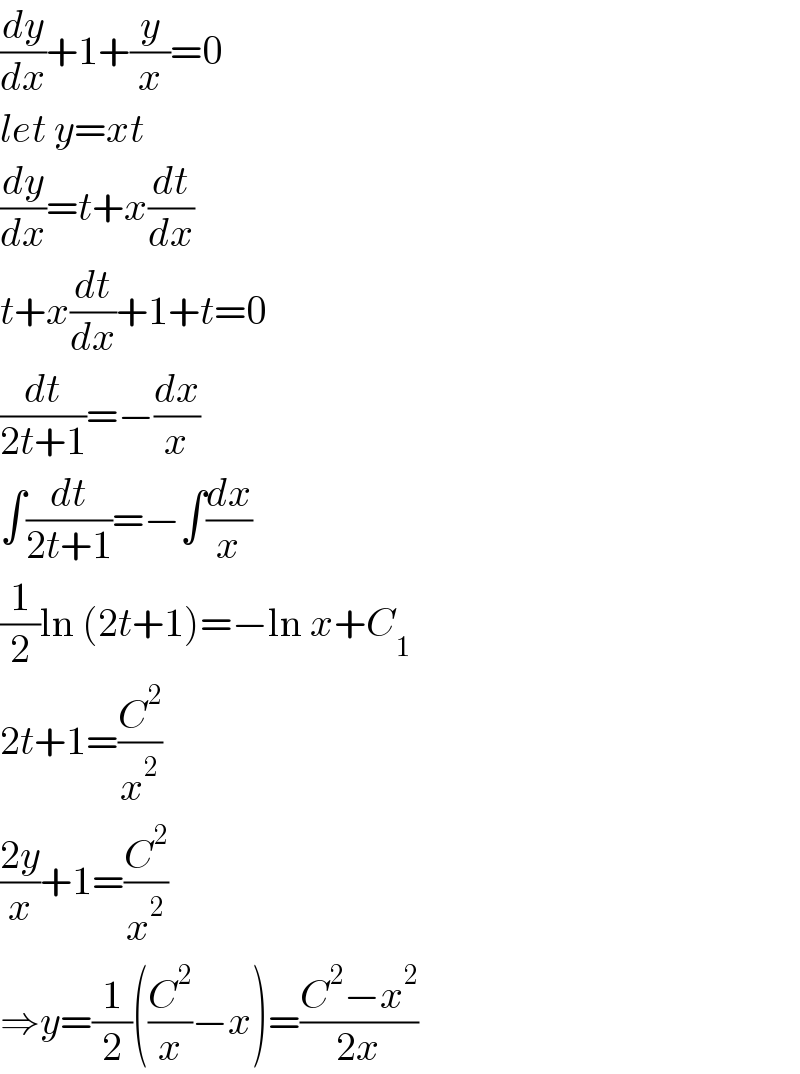
$$\frac{{dy}}{{dx}}+\mathrm{1}+\frac{{y}}{{x}}=\mathrm{0} \\ $$$${let}\:{y}={xt} \\ $$$$\frac{{dy}}{{dx}}={t}+{x}\frac{{dt}}{{dx}} \\ $$$${t}+{x}\frac{{dt}}{{dx}}+\mathrm{1}+{t}=\mathrm{0} \\ $$$$\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}}=−\frac{{dx}}{{x}} \\ $$$$\int\frac{{dt}}{\mathrm{2}{t}+\mathrm{1}}=−\int\frac{{dx}}{{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}{t}+\mathrm{1}\right)=−\mathrm{ln}\:{x}+{C}_{\mathrm{1}} \\ $$$$\mathrm{2}{t}+\mathrm{1}=\frac{{C}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}{y}}{{x}}+\mathrm{1}=\frac{{C}^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{C}^{\mathrm{2}} }{{x}}−{x}\right)=\frac{{C}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{2}{x}} \\ $$
Commented by Calculusboy last updated on 30/Dec/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
