
Previous in Relation and Functions Next in Relation and Functions
Question Number 202536 by cortano12 last updated on 29/Dec/23

$$\:\:\: \\ $$
Answered by taguim001 last updated on 29/Dec/23
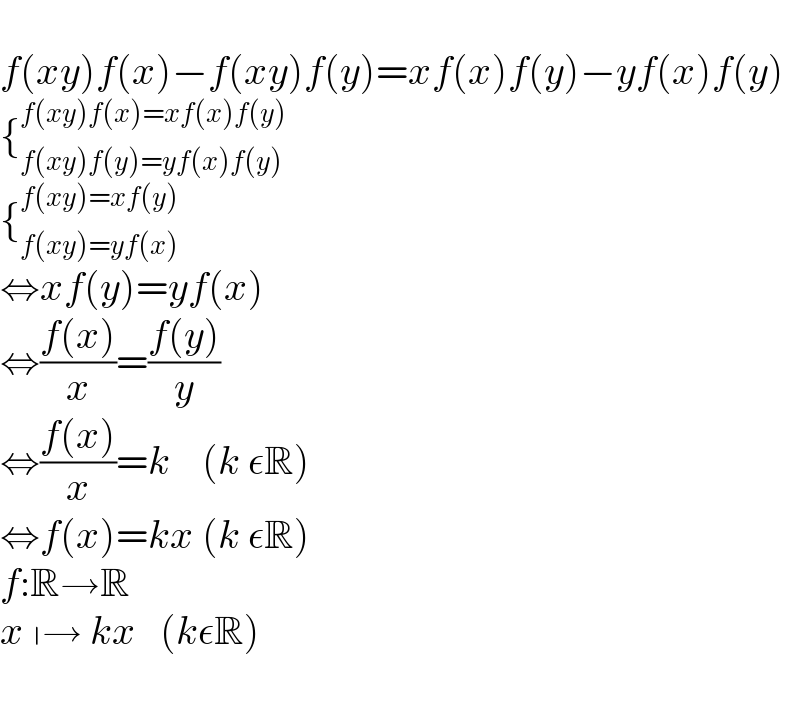
$$ \\ $$$${f}\left({xy}\right){f}\left({x}\right)−{f}\left({xy}\right){f}\left({y}\right)={xf}\left({x}\right){f}\left({y}\right)−{yf}\left({x}\right){f}\left({y}\right) \\ $$$$\left\{_{{f}\left({xy}\right){f}\left({y}\right)={yf}\left({x}\right){f}\left({y}\right)} ^{{f}\left({xy}\right){f}\left({x}\right)={xf}\left({x}\right){f}\left({y}\right)} \right. \\ $$$$\left\{_{{f}\left({xy}\right)={yf}\left({x}\right)} ^{{f}\left({xy}\right)={xf}\left({y}\right)} \right. \\ $$$$\Leftrightarrow{xf}\left({y}\right)={yf}\left({x}\right) \\ $$$$\Leftrightarrow\frac{{f}\left({x}\right)}{{x}}=\frac{{f}\left({y}\right)}{{y}} \\ $$$$\Leftrightarrow\frac{{f}\left({x}\right)}{{x}}={k}\:\:\:\:\left({k}\:\epsilon\mathbb{R}\right) \\ $$$$\Leftrightarrow{f}\left({x}\right)={kx}\:\left({k}\:\epsilon\mathbb{R}\right) \\ $$$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${x}\:\shortmid\rightarrow\:{kx}\:\:\:\left({k}\epsilon\mathbb{R}\right) \\ $$$$ \\ $$
Answered by witcher3 last updated on 30/Dec/23
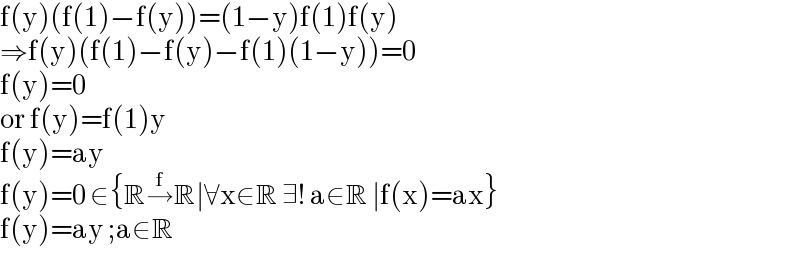
$$\mathrm{f}\left(\mathrm{y}\right)\left(\mathrm{f}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{y}\right)\right)=\left(\mathrm{1}−\mathrm{y}\right)\mathrm{f}\left(\mathrm{1}\right)\mathrm{f}\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{y}\right)\left(\mathrm{f}\left(\mathrm{1}\right)−\mathrm{f}\left(\mathrm{y}\right)−\mathrm{f}\left(\mathrm{1}\right)\left(\mathrm{1}−\mathrm{y}\right)\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{y}\right)=\mathrm{0} \\ $$$$\mathrm{or}\:\mathrm{f}\left(\mathrm{y}\right)=\mathrm{f}\left(\mathrm{1}\right)\mathrm{y} \\ $$$$\mathrm{f}\left(\mathrm{y}\right)=\mathrm{ay} \\ $$$$\mathrm{f}\left(\mathrm{y}\right)=\mathrm{0}\:\in\left\{\mathbb{R}\overset{\mathrm{f}} {\rightarrow}\mathbb{R}\mid\forall\mathrm{x}\in\mathbb{R}\:\exists!\:\mathrm{a}\in\mathbb{R}\:\mid\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}\right\} \\ $$$$\mathrm{f}\left(\mathrm{y}\right)=\mathrm{ay}\:;\mathrm{a}\in\mathbb{R} \\ $$
