Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 202500 by Calculusboy last updated on 28/Dec/23

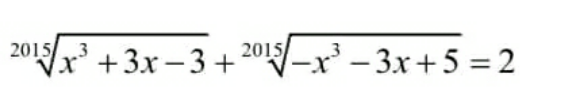
Answered by Frix last updated on 28/Dec/23

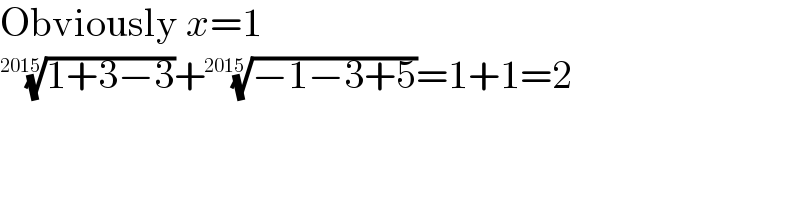
Obviously x=1 ((1+3−3))^(1/(2015)) +((−1−3+5))^(1/(2015)) =1+1=2

$$\mathrm{Obviously}\:{x}=\mathrm{1} \\ $$$$\sqrt[{\mathrm{2015}}]{\mathrm{1}+\mathrm{3}−\mathrm{3}}+\sqrt[{\mathrm{2015}}]{−\mathrm{1}−\mathrm{3}+\mathrm{5}}=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$

Answered by Rasheed.Sindhi last updated on 28/Dec/23

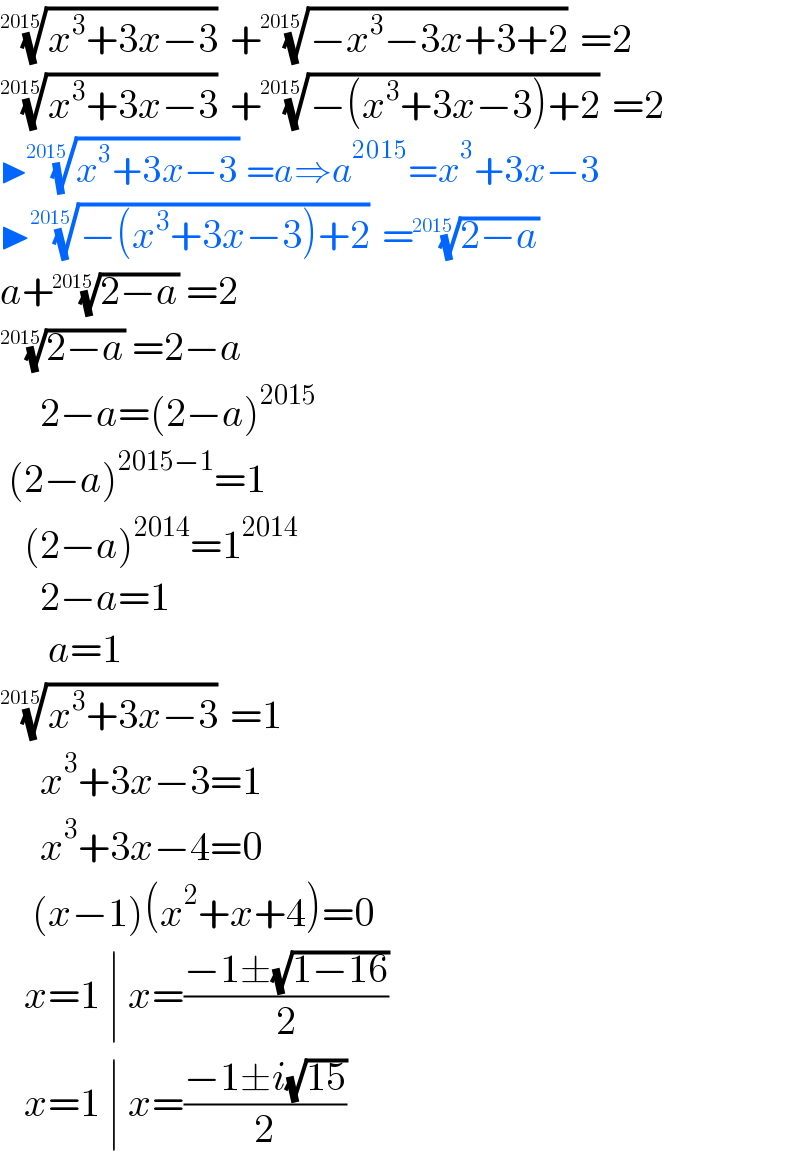
((x^3 +3x−3))^(1/(2015)) +((−x^3 −3x+3+2))^(1/(2015)) =2 ((x^3 +3x−3))^(1/(2015)) +((−(x^3 +3x−3)+2))^(1/(2015)) =2 ▶((x^3 +3x−3))^(1/(2015)) =a⇒a^(2015) =x^3 +3x−3 ▶((−(x^3 +3x−3)+2))^(1/(2015)) =((2−a))^(1/(2015)) a+((2−a))^(1/(2015)) =2 ((2−a))^(1/(2015)) =2−a 2−a=(2−a)^(2015) (2−a)^(2015−1) =1 (2−a)^(2014) =1^(2014) 2−a=1 a=1 ((x^3 +3x−3))^(1/(2015)) =1 x^3 +3x−3=1 x^3 +3x−4=0 (x−1)(x^2 +x+4)=0 x=1 ∣ x=((−1±(√(1−16)))/2) x=1 ∣ x=((−1±i(√(15)))/2)

$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:+\sqrt[{\mathrm{2015}}]{−{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{3}+\mathrm{2}}\:=\mathrm{2} \\ $$$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:+\sqrt[{\mathrm{2015}}]{−\left({x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}\right)+\mathrm{2}}\:=\mathrm{2} \\ $$$$\blacktriangleright\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:={a}\Rightarrow{a}^{\mathrm{2015}} ={x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3} \\ $$$$\blacktriangleright\sqrt[{\mathrm{2015}}]{−\left({x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}\right)+\mathrm{2}}\:=\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}}\: \\ $$$${a}+\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}}\:=\mathrm{2} \\ $$$$\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}}\:=\mathrm{2}−{a} \\ $$$$\:\:\:\:\:\mathrm{2}−{a}=\left(\mathrm{2}−{a}\right)^{\mathrm{2015}} \\ $$$$\:\left(\mathrm{2}−{a}\right)^{\mathrm{2015}−\mathrm{1}} =\mathrm{1} \\ $$$$\:\:\:\left(\mathrm{2}−{a}\right)^{\mathrm{2014}} =\mathrm{1}^{\mathrm{2014}} \\ $$$$\:\:\:\:\:\mathrm{2}−{a}=\mathrm{1} \\ $$$$\:\:\:\:\:\:{a}=\mathrm{1} \\ $$$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:=\mathrm{1} \\ $$$$\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}=\mathrm{1} \\ $$$$\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\:\:\:{x}=\mathrm{1}\:\mid\:{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{16}}}{\mathrm{2}} \\ $$$$\:\:\:{x}=\mathrm{1}\:\mid\:{x}=\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{15}}}{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 28/Dec/23

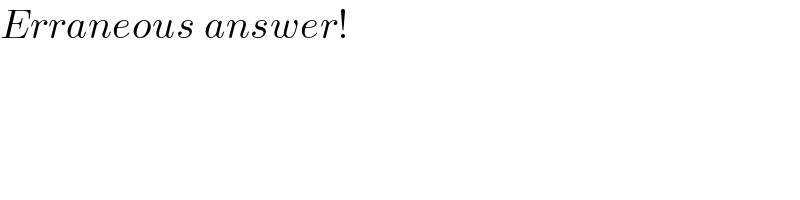
Erraneous answer!

$${Erraneous}\:{answer}! \\ $$

Commented by Frix last updated on 28/Dec/23

I think we need (√1)+(√1)=2 ⇒ x^3 +3x−4=1 and your solution is right. I don′t think solutions for ((re^(iθ) ))^(1/n) +((2−re^(iθ) ))^(1/n) ∈R exist when re^(iθ) ∉R

$$\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{need}\:\sqrt{\mathrm{1}}+\sqrt{\mathrm{1}}=\mathrm{2}\:\Rightarrow \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{right}. \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{solutions}\:\mathrm{for} \\ $$$$\sqrt[{{n}}]{{r}\mathrm{e}^{\mathrm{i}\theta} }+\sqrt[{{n}}]{\mathrm{2}−{r}\mathrm{e}^{\mathrm{i}\theta} }\in\mathbb{R} \\ $$$$\mathrm{exist}\:\mathrm{when}\:{r}\mathrm{e}^{\mathrm{i}\theta} \notin\mathbb{R} \\ $$

Commented by esmaeil last updated on 28/Dec/23

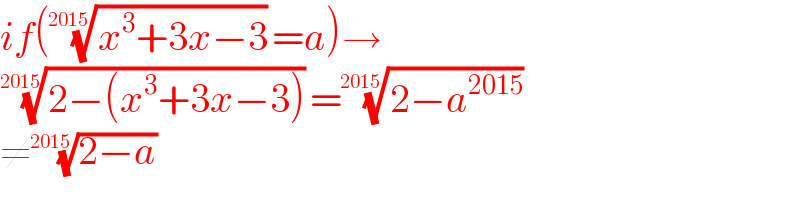
if(((x^3 +3x−3))^(1/(2015)) =a)→ ((2−(x^3 +3x−3)))^(1/(2015)) =((2−a^(2015) ))^(1/(2015)) ≠((2−a))^(1/(2015))

$${if}\left(\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}={a}\right)\rightarrow \\ $$$$\sqrt[{\mathrm{2015}}]{\mathrm{2}−\left({x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}\right)}=\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}^{\mathrm{2015}} } \\ $$$$\neq\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}} \\ $$

Commented by Frix last updated on 28/Dec/23

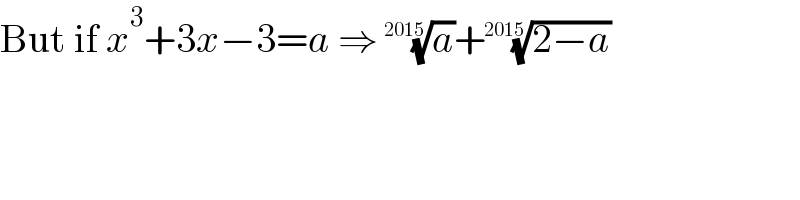
But if x^3 +3x−3=a ⇒ (a)^(1/(2015)) +((2−a))^(1/(2015))

$$\mathrm{But}\:\mathrm{if}\:{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}={a}\:\Rightarrow\:\sqrt[{\mathrm{2015}}]{{a}}+\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}} \\ $$

Commented by esmaeil last updated on 28/Dec/23

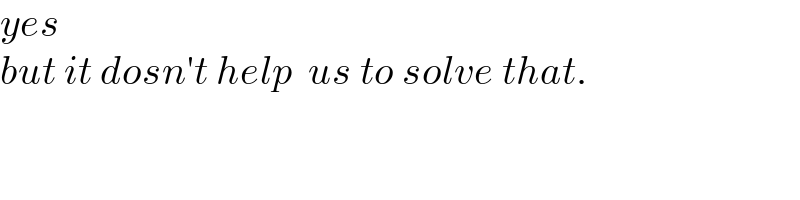
yes but it dosn′t help us to solve that.

$${yes} \\ $$$${but}\:{it}\:{dosn}'{t}\:{help}\:\:{us}\:{to}\:{solve}\:{that}. \\ $$

Commented by Frix last updated on 28/Dec/23

It helps to see there′s no other solutions besides a=1.

$$\mathrm{It}\:\mathrm{helps}\:\mathrm{to}\:\mathrm{see}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{other}\:\mathrm{solutions} \\ $$$$\mathrm{besides}\:{a}=\mathrm{1}. \\ $$

Commented by Calculusboy last updated on 28/Dec/23

thanks sir

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Dec/23

Thanks sir for guidance!

$$\mathbb{T}\boldsymbol{\mathrm{hanks}}\:\boldsymbol{\mathrm{sir}}\:\mathrm{for}\:\boldsymbol{\mathrm{guidance}}! \\ $$

Answered by Rasheed.Sindhi last updated on 28/Dec/23

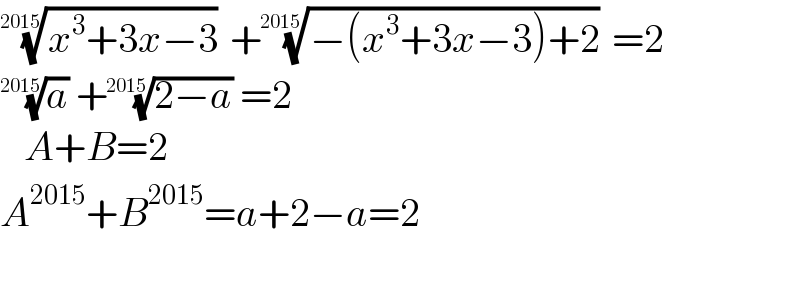
((x^3 +3x−3))^(1/(2015)) +((−(x^3 +3x−3)+2))^(1/(2015)) =2 (a)^(1/(2015)) +((2−a))^(1/(2015)) =2 A+B=2 A^(2015) +B^(2015) =a+2−a=2

$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:+\sqrt[{\mathrm{2015}}]{−\left({x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}\right)+\mathrm{2}}\:=\mathrm{2} \\ $$$$\sqrt[{\mathrm{2015}}]{{a}}\:+\sqrt[{\mathrm{2015}}]{\mathrm{2}−{a}}\:=\mathrm{2} \\ $$$$\:\:\:{A}+{B}=\mathrm{2} \\ $$$${A}^{\mathrm{2015}} +{B}^{\mathrm{2015}} ={a}+\mathrm{2}−{a}=\mathrm{2} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 29/Dec/23

According to the strategy of sir Frix ((x^3 +3x−3))^(1/(2015)) +((−x^3 −3x+5))^(1/(2015)) ((x^3 +3x−4+1))^(1/(2015)) +((−(x^3 +3x−4)+1))^(1/(2015)) x^3 +3x−4=y ((1+y))^(1/(2015)) +((1−y))^(1/(2015)) =2 One possibility: ((1+y))^(1/(2015)) +((1−y))^(1/(2015)) =1+1 ((1+y))^(1/(2015)) =1 ∧ ((1−y))^(1/(2015)) =1 1+y=1^(2015) ∧ 1−y=1^(2015) 1+y=1 ∧ 1−y=1⇒y=0 x^3 +3x−4=0 (x−1)(x^2 +x+4)=0 x=1 , ((−1±i(√(15)) )/2)

$$\boldsymbol{\mathrm{According}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{strategy}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{Frix}} \\ $$$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{3}}\:+\sqrt[{\mathrm{2015}}]{−{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{5}} \\ $$$$\: \\ $$$$\sqrt[{\mathrm{2015}}]{{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}+\mathrm{1}}\:+\sqrt[{\mathrm{2015}}]{−\left({x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}\right)+\mathrm{1}} \\ $$$${x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}={y} \\ $$$$\sqrt[{\mathrm{2015}}]{\mathrm{1}+{y}}\:+\sqrt[{\mathrm{2015}}]{\mathrm{1}−{y}}\:=\mathrm{2} \\ $$$${One}\:{possibility}: \\ $$$$\sqrt[{\mathrm{2015}}]{\mathrm{1}+{y}}\:+\sqrt[{\mathrm{2015}}]{\mathrm{1}−{y}}\:=\mathrm{1}+\mathrm{1} \\ $$$$\:\:\:\sqrt[{\mathrm{2015}}]{\mathrm{1}+{y}}\:=\mathrm{1}\:\wedge\:\sqrt[{\mathrm{2015}}]{\mathrm{1}−{y}}\:=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}+{y}=\mathrm{1}^{\mathrm{2015}} \:\:\:\wedge\:\mathrm{1}−{y}=\mathrm{1}^{\mathrm{2015}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}+{y}=\mathrm{1}\:\:\:\wedge\:\mathrm{1}−{y}=\mathrm{1}\Rightarrow{y}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{3}} +\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:{x}=\mathrm{1}\:,\:\:\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{15}}\:}{\mathrm{2}} \\ $$

Commented by mr W last updated on 29/Dec/23

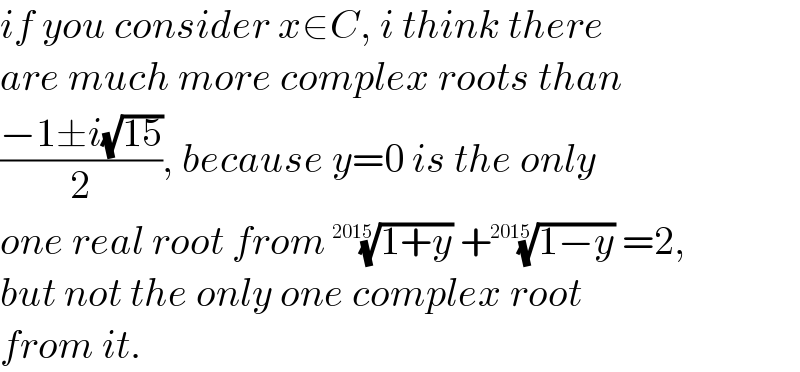
if you consider x∈C, i think there are much more complex roots than ((−1±i(√(15)))/2), because y=0 is the only one real root from ((1+y))^(1/(2015)) +((1−y))^(1/(2015)) =2, but not the only one complex root from it.

$${if}\:{you}\:{consider}\:{x}\in{C},\:{i}\:{think}\:{there}\: \\ $$$${are}\:{much}\:{more}\:{complex}\:{roots}\:{than} \\ $$$$\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{15}}}{\mathrm{2}},\:{because}\:{y}=\mathrm{0}\:{is}\:{the}\:{only}\: \\ $$$${one}\:{real}\:{root}\:{from}\:\sqrt[{\mathrm{2015}}]{\mathrm{1}+{y}}\:+\sqrt[{\mathrm{2015}}]{\mathrm{1}−{y}}\:=\mathrm{2}, \\ $$$${but}\:{not}\:{the}\:{only}\:{one}\:{complex}\:{root}\: \\ $$$${from}\:{it}. \\ $$

Commented by Frix last updated on 29/Dec/23

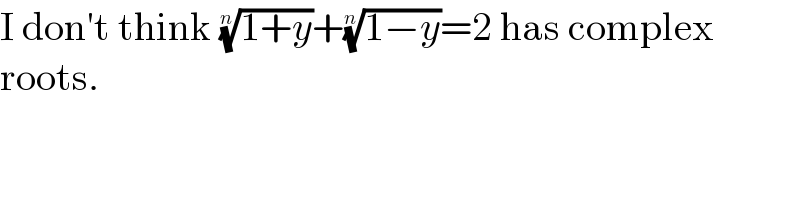
I don′t think ((1+y))^(1/n) +((1−y))^(1/n) =2 has complex roots.

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\sqrt[{{n}}]{\mathrm{1}+{y}}+\sqrt[{{n}}]{\mathrm{1}−{y}}=\mathrm{2}\:\mathrm{has}\:\mathrm{complex} \\ $$$$\mathrm{roots}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com