Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 202406 by mou0113 last updated on 26/Dec/23

Answered by witcher3 last updated on 26/Dec/23

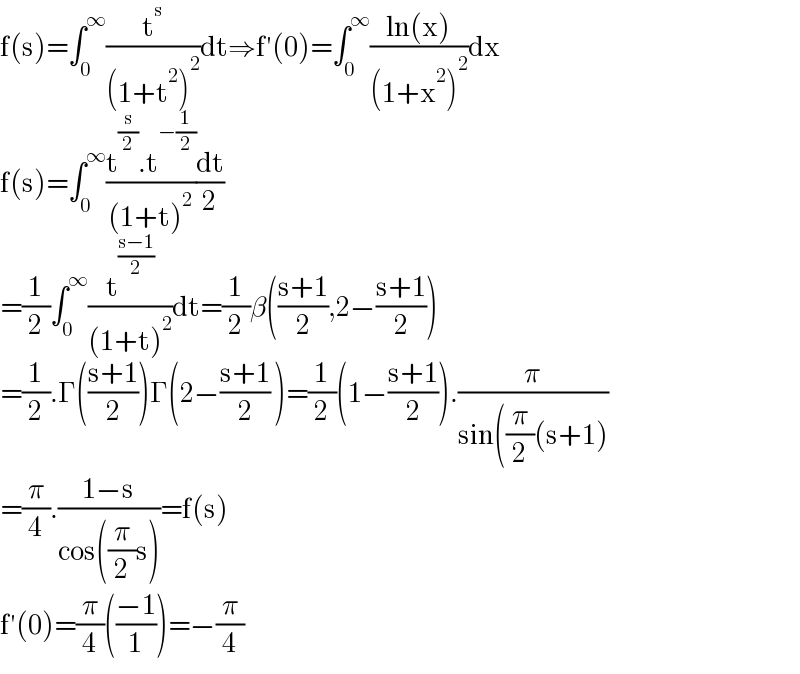
f(s)=∫_0 ^∞ (t^s /((1+t^2 )^2 ))dt⇒f′(0)=∫_0 ^∞ ((ln(x))/((1+x^2 )^2 ))dx f(s)=∫_0 ^∞ ((t^(s/2) .t^(−(1/2)) )/((1+t)^2 ))(dt/2) =(1/2)∫_0 ^∞ (t^((s−1)/2) /((1+t)^2 ))dt=(1/2)β(((s+1)/2),2−((s+1)/2)) =(1/2).Γ(((s+1)/2))Γ(2−((s+1)/2) )=(1/2)(1−((s+1)/2)).(π/(sin((π/2)(s+1))) =(π/4).((1−s)/(cos((π/2)s)))=f(s) f′(0)=(π/4)(((−1)/1))=−(π/4)

$$\mathrm{f}\left(\mathrm{s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{s}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\Rightarrow\mathrm{f}'\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{s}}{\mathrm{2}}} .\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\frac{\mathrm{dt}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\frac{\mathrm{s}−\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{s}+\mathrm{1}}{\mathrm{2}},\mathrm{2}−\frac{\mathrm{s}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\Gamma\left(\frac{\mathrm{s}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{2}−\frac{\mathrm{s}+\mathrm{1}}{\mathrm{2}}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{s}+\mathrm{1}}{\mathrm{2}}\right).\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\left(\mathrm{s}+\mathrm{1}\right)\right.} \\ $$$$=\frac{\pi}{\mathrm{4}}.\frac{\mathrm{1}−\mathrm{s}}{\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\mathrm{s}\right)}=\mathrm{f}\left(\mathrm{s}\right) \\ $$$$\mathrm{f}'\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{4}}\left(\frac{−\mathrm{1}}{\mathrm{1}}\right)=−\frac{\pi}{\mathrm{4}} \\ $$

Commented by mou0113 last updated on 26/Dec/23

thank you

$${thank}\:{you} \\ $$

Answered by Mathspace last updated on 26/Dec/23

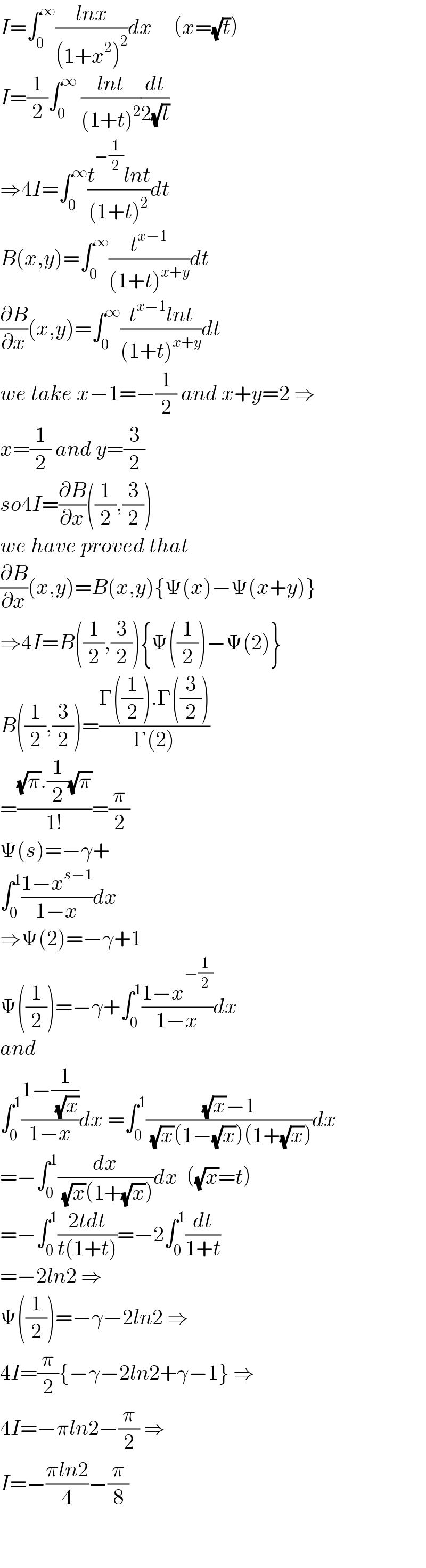
I=∫_0 ^∞ ((lnx)/((1+x^2 )^2 ))dx (x=(√t)) I=(1/2)∫_0 ^∞ ((lnt)/((1+t)^2 ))(dt/(2(√t))) ⇒4I=∫_0 ^∞ ((t^(−(1/2)) lnt)/((1+t)^2 ))dt B(x,y)=∫_0 ^∞ (t^(x−1) /((1+t)^(x+y) ))dt (∂B/∂x)(x,y)=∫_0 ^∞ ((t^(x−1) lnt)/((1+t)^(x+y) ))dt we take x−1=−(1/2) and x+y=2 ⇒ x=(1/2) and y=(3/2) so4I=(∂B/∂x)((1/2),(3/2)) we have proved that (∂B/∂x)(x,y)=B(x,y){Ψ(x)−Ψ(x+y)} ⇒4I=B((1/2),(3/2)){Ψ((1/2))−Ψ(2)} B((1/2),(3/2))=((Γ((1/2)).Γ((3/2)))/(Γ(2))) =(((√π).(1/2)(√π))/(1!))=(π/2) Ψ(s)=−γ+ ∫_0 ^1 ((1−x^(s−1) )/(1−x))dx ⇒Ψ(2)=−γ+1 Ψ((1/2))=−γ+∫_0 ^1 ((1−x^(−(1/2)) )/(1−x))dx and ∫_0 ^1 ((1−(1/( (√x))))/(1−x))dx =∫_0 ^1 (((√x)−1)/( (√x)(1−(√x))(1+(√x))))dx =−∫_0 ^1 (dx/( (√x)(1+(√x))))dx ((√x)=t) =−∫_0 ^1 ((2tdt)/(t(1+t)))=−2∫_0 ^1 (dt/(1+t)) =−2ln2 ⇒ Ψ((1/2))=−γ−2ln2 ⇒ 4I=(π/2){−γ−2ln2+γ−1} ⇒ 4I=−πln2−(π/2) ⇒ I=−((πln2)/4)−(π/8)

$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\:\:\:\:\left({x}=\sqrt{{t}}\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{{lnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\frac{{dt}}{\mathrm{2}\sqrt{{t}}} \\ $$$$\Rightarrow\mathrm{4}{I}=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} {lnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$${B}\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{{x}+{y}} }{dt} \\ $$$$\frac{\partial{B}}{\partial{x}}\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} {lnt}}{\left(\mathrm{1}+{t}\right)^{{x}+{y}} }{dt}\: \\ $$$${we}\:{take}\:{x}−\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{x}+{y}=\mathrm{2}\:\Rightarrow \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{y}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${so}\mathrm{4}{I}=\frac{\partial{B}}{\partial{x}}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$${we}\:{have}\:{proved}\:{that} \\ $$$$\frac{\partial{B}}{\partial{x}}\left({x},{y}\right)={B}\left({x},{y}\right)\left\{\Psi\left({x}\right)−\Psi\left({x}+{y}\right)\right\} \\ $$$$\Rightarrow\mathrm{4}{I}={B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\left\{\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\mathrm{2}\right)\right\} \\ $$$${B}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)} \\ $$$$=\frac{\sqrt{\pi}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}}{\mathrm{1}!}=\frac{\pi}{\mathrm{2}} \\ $$$$\Psi\left({s}\right)=−\gamma+ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{s}−\mathrm{1}} }{\mathrm{1}−{x}}{dx} \\ $$$$\Rightarrow\Psi\left(\mathrm{2}\right)=−\gamma+\mathrm{1} \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{x}}{dx} \\ $$$${and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{{x}}}}{\mathrm{1}−{x}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{{x}}−\mathrm{1}}{\:\sqrt{{x}}\left(\mathrm{1}−\sqrt{{x}}\right)\left(\mathrm{1}+\sqrt{{x}}\right)}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}\left(\mathrm{1}+\sqrt{{x}}\right)}{dx}\:\:\left(\sqrt{{x}}={t}\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{tdt}}{{t}\left(\mathrm{1}+{t}\right)}=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}} \\ $$$$=−\mathrm{2}{ln}\mathrm{2}\:\Rightarrow \\ $$$$\Psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma−\mathrm{2}{ln}\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{4}{I}=\frac{\pi}{\mathrm{2}}\left\{−\gamma−\mathrm{2}{ln}\mathrm{2}+\gamma−\mathrm{1}\right\}\:\Rightarrow \\ $$$$\mathrm{4}{I}=−\pi{ln}\mathrm{2}−\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${I}=−\frac{\pi{ln}\mathrm{2}}{\mathrm{4}}−\frac{\pi}{\mathrm{8}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com