
Question Number 202340 by hardmath last updated on 24/Dec/23
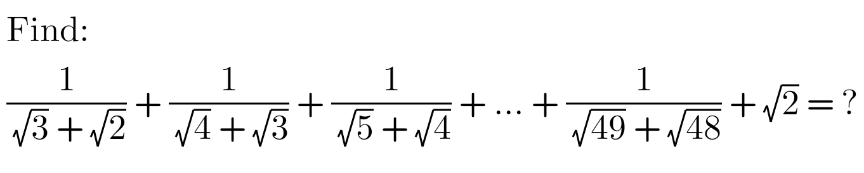
Answered by MATHEMATICSAM last updated on 25/Dec/23
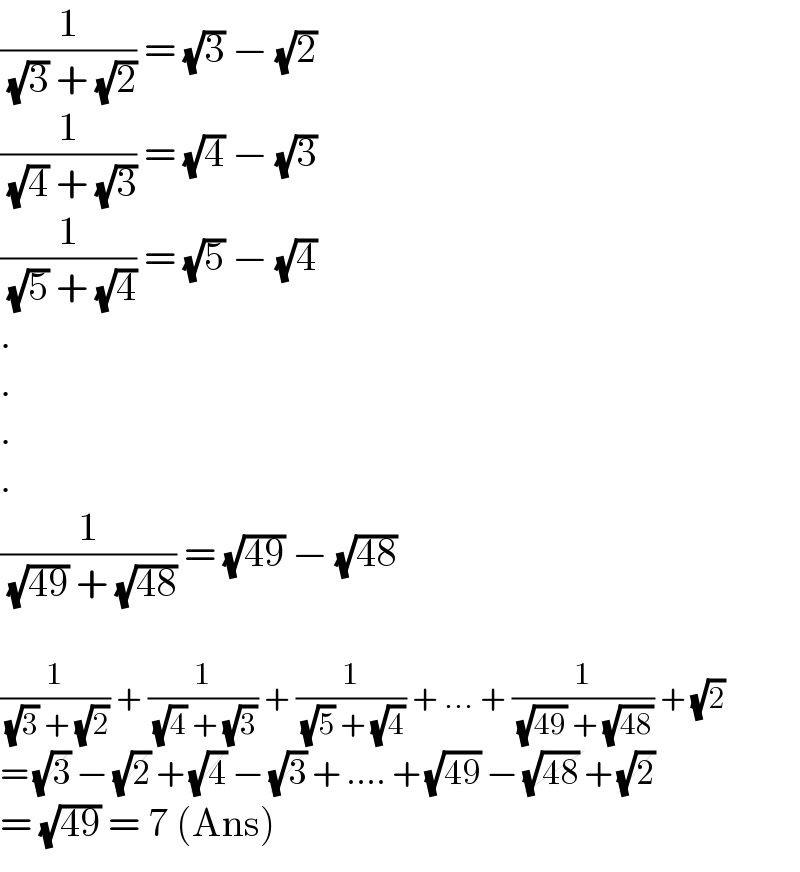
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:+\:\sqrt{\mathrm{2}}}\:=\:\sqrt{\mathrm{3}}\:−\:\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}\:+\:\sqrt{\mathrm{3}}}\:=\:\sqrt{\mathrm{4}}\:−\:\sqrt{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}\:+\:\sqrt{\mathrm{4}}}\:=\:\sqrt{\mathrm{5}}\:−\:\sqrt{\mathrm{4}} \\ $$$$. \\ $$$$. \\ $$$$. \\ $$$$. \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{49}}\:+\:\sqrt{\mathrm{48}}}\:=\:\sqrt{\mathrm{49}}\:−\:\sqrt{\mathrm{48}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:+\:\sqrt{\mathrm{2}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}\:+\:\sqrt{\mathrm{3}}}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}\:+\:\sqrt{\mathrm{4}}}\:+\:...\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{49}}\:+\:\sqrt{\mathrm{48}}}\:+\:\sqrt{\mathrm{2}} \\ $$$$=\:\cancel{\sqrt{\mathrm{3}}}\:−\:\cancel{\sqrt{\mathrm{2}}}\:+\:\cancel{\sqrt{\mathrm{4}}}\:−\:\cancel{\sqrt{\mathrm{3}}}\:+\:....\:+\:\sqrt{\mathrm{49}}\:−\:\cancel{\sqrt{\mathrm{48}}\:}+\:\cancel{\sqrt{\mathrm{2}}} \\ $$$$=\:\sqrt{\mathrm{49}}\:=\:\mathrm{7}\:\left(\mathrm{Ans}\right) \\ $$
Commented by hardmath last updated on 25/Dec/23
$$\mathrm{thankyou}\:\mathrm{dear}\:\mathrm{professors} \\ $$
Answered by Frix last updated on 24/Dec/23
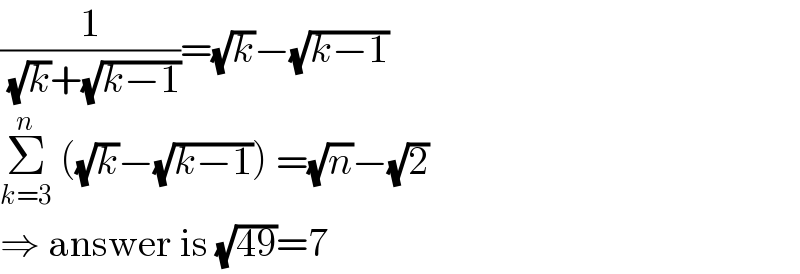
$$\frac{\mathrm{1}}{\:\sqrt{{k}}+\sqrt{{k}−\mathrm{1}}}=\sqrt{{k}}−\sqrt{{k}−\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{3}} {\overset{{n}} {\sum}}\:\left(\sqrt{{k}}−\sqrt{{k}−\mathrm{1}}\right)\:=\sqrt{{n}}−\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\sqrt{\mathrm{49}}=\mathrm{7} \\ $$
