
Question Number 202127 by Calculusboy last updated on 21/Dec/23
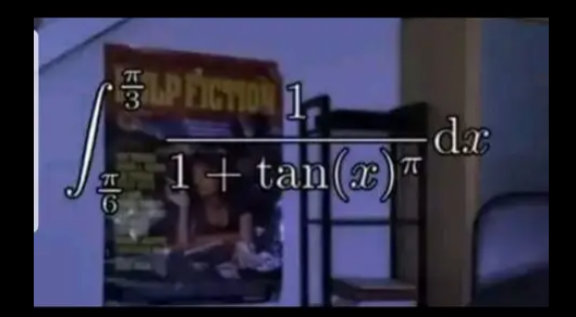
Answered by qaz last updated on 21/Dec/23
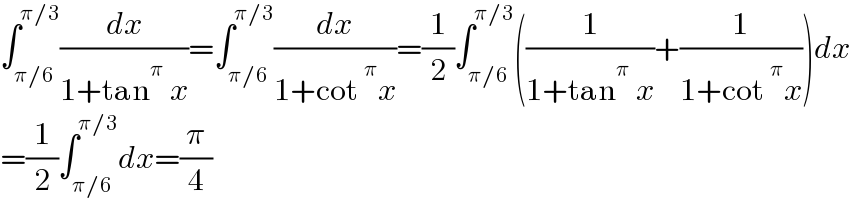
$$\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{{dx}}{\mathrm{1}+\mathrm{tan}^{\pi} \:{x}}=\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{{dx}}{\mathrm{1}+\mathrm{cot}\:^{\pi} {x}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\pi} \:{x}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cot}\:^{\pi} {x}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} {dx}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by Calculusboy last updated on 22/Dec/23
$$\boldsymbol{{nice}}\:\boldsymbol{{solution}}\:\boldsymbol{{sir}} \\ $$
