
Question Number 201956 by sonukgindia last updated on 16/Dec/23
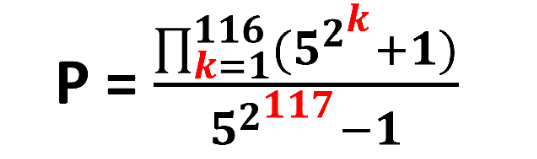
Commented by mahdipoor last updated on 16/Dec/23
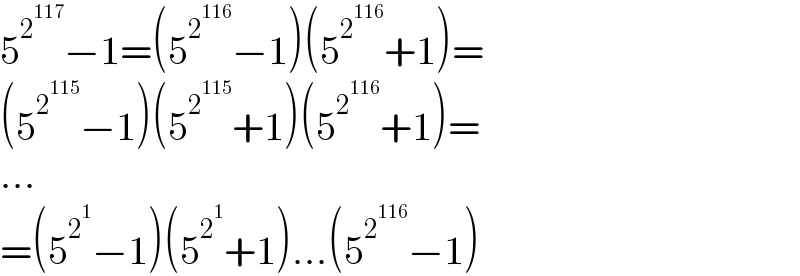
$$\mathrm{5}^{\mathrm{2}^{\mathrm{117}} } −\mathrm{1}=\left(\mathrm{5}^{\mathrm{2}^{\mathrm{116}} } −\mathrm{1}\right)\left(\mathrm{5}^{\mathrm{2}^{\mathrm{116}} } +\mathrm{1}\right)= \\ $$$$\left(\mathrm{5}^{\mathrm{2}^{\mathrm{115}} } −\mathrm{1}\right)\left(\mathrm{5}^{\mathrm{2}^{\mathrm{115}} } +\mathrm{1}\right)\left(\mathrm{5}^{\mathrm{2}^{\mathrm{116}} } +\mathrm{1}\right)= \\ $$$$... \\ $$$$=\left(\mathrm{5}^{\mathrm{2}^{\mathrm{1}} } −\mathrm{1}\right)\left(\mathrm{5}^{\mathrm{2}^{\mathrm{1}} } +\mathrm{1}\right)...\left(\mathrm{5}^{\mathrm{2}^{\mathrm{116}} } −\mathrm{1}\right) \\ $$
Answered by deleteduser1 last updated on 16/Dec/23

$$\left(\mathrm{5}^{\mathrm{2}} −\mathrm{1}\right){P}=\mathrm{1}\Rightarrow{P}=\frac{\mathrm{1}}{\mathrm{24}} \\ $$
Commented by Frix last updated on 17/Dec/23

$$\mathrm{Yes}! \\ $$
