
Question Number 201947 by Mingma last updated on 16/Dec/23
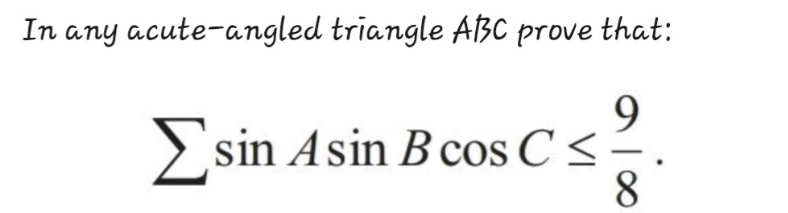
Answered by Frix last updated on 18/Dec/23
![sin α sin β cos (π−α−β) + +sin β sin (π−α−β) cos α + +sin (π−α−β) sin α cos β = =((3−(cos 2α +cos 2β +cos 2(α+β))/4)= [Let α=u−v∧β=u+v] =((3−(cos 4u +cos 2(u−v) +cos 2(u−v) )/4) (d/dv)[((3−(cos 4u +cos 2(u−v) +cos 2(u−v) )/4)]=0 ((sin 2(u+v) −sin 2(u−v))/2)=0 sin 2(u+v) =sin 2(u−v) 0≤v<(π/2) ⇒ v=0 ⇒ ((3−(cos 4u +cos 2(u−v) +cos 2(u−v) )/4)= =((3−(cos 4u +2cos 2u))/4) (d/du)[((3−(cos 4u +2cos 2u))/4)]=0 sin 4u +sin 2u =0 −2cos u sin u (1−2cos u)(1+2cos u)=0 0<u≤(π/2) ⇒ u=(π/3)[∨u=(π/2) ⇒ α=β=(π/2) impossible] ⇒ α=β=(π/3) ⇒ max (((3−(cos 2α +cos 2β +cos 2(α+β))/4))=(9/8)](Q201987.png)
$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\left(\pi−\alpha−\beta\right)\:+ \\ $$$$\:\:\:\:\:+\mathrm{sin}\:\beta\:\mathrm{sin}\:\left(\pi−\alpha−\beta\right)\:\mathrm{cos}\:\alpha\:+ \\ $$$$\:\:\:\:\:+\mathrm{sin}\:\left(\pi−\alpha−\beta\right)\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:= \\ $$$$=\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{2}\alpha\:+\mathrm{cos}\:\mathrm{2}\beta\:+\mathrm{cos}\:\mathrm{2}\left(\alpha+\beta\right)\right.}{\mathrm{4}}= \\ $$$$\:\:\:\:\:\left[\mathrm{Let}\:\alpha={u}−{v}\wedge\beta={u}+{v}\right] \\ $$$$=\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{4}{u}\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:\right.}{\mathrm{4}} \\ $$$$\frac{{d}}{{dv}}\left[\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{4}{u}\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:\right.}{\mathrm{4}}\right]=\mathrm{0} \\ $$$$\frac{\mathrm{sin}\:\mathrm{2}\left({u}+{v}\right)\:−\mathrm{sin}\:\mathrm{2}\left({u}−{v}\right)}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{2}\left({u}+{v}\right)\:=\mathrm{sin}\:\mathrm{2}\left({u}−{v}\right) \\ $$$$\mathrm{0}\leqslant{v}<\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{v}=\mathrm{0}\:\Rightarrow \\ $$$$\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{4}{u}\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:+\mathrm{cos}\:\mathrm{2}\left({u}−{v}\right)\:\right.}{\mathrm{4}}= \\ $$$$=\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{4}{u}\:+\mathrm{2cos}\:\mathrm{2}{u}\right)}{\mathrm{4}} \\ $$$$\frac{{d}}{{du}}\left[\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{4}{u}\:+\mathrm{2cos}\:\mathrm{2}{u}\right)}{\mathrm{4}}\right]=\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{4}{u}\:+\mathrm{sin}\:\mathrm{2}{u}\:=\mathrm{0} \\ $$$$−\mathrm{2cos}\:{u}\:\mathrm{sin}\:{u}\:\left(\mathrm{1}−\mathrm{2cos}\:{u}\right)\left(\mathrm{1}+\mathrm{2cos}\:{u}\right)=\mathrm{0} \\ $$$$\mathrm{0}<{u}\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{u}=\frac{\pi}{\mathrm{3}}\left[\vee{u}=\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\alpha=\beta=\frac{\pi}{\mathrm{2}}\:\mathrm{impossible}\right] \\ $$$$\Rightarrow\:\alpha=\beta=\frac{\pi}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{max}\:\left(\frac{\mathrm{3}−\left(\mathrm{cos}\:\mathrm{2}\alpha\:+\mathrm{cos}\:\mathrm{2}\beta\:+\mathrm{cos}\:\mathrm{2}\left(\alpha+\beta\right)\right.}{\mathrm{4}}\right)=\frac{\mathrm{9}}{\mathrm{8}} \\ $$
Commented by Mingma last updated on 18/Dec/23
Perfect ��
