
Question Number 201907 by mnjuly1970 last updated on 15/Dec/23
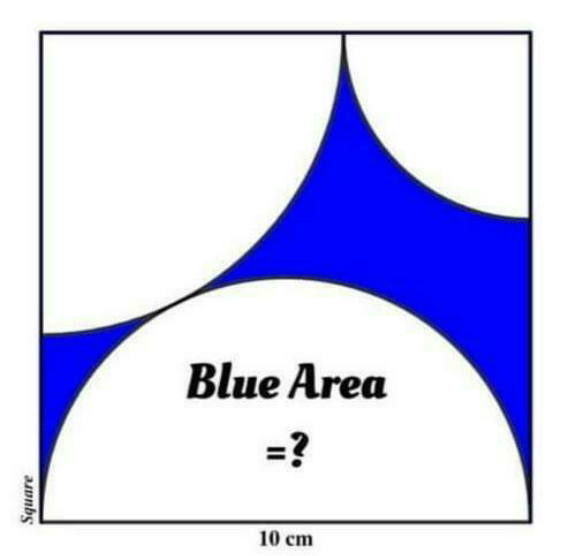
Answered by Rasheed.Sindhi last updated on 15/Dec/23

$$\bullet{Radius}\:{of}\:{Semi}-{circle}\:{R}=\:\frac{\mathrm{10}}{\mathrm{2}}=\mathrm{5}\:{cm} \\ $$$$\bullet{let}\:{radous}\:{of}\:{greater}\:{quarter}-{circle}={r}_{\mathrm{1}} \\ $$$$\left({R}+{r}_{\mathrm{1}} \right)^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} =\mathrm{125} \\ $$$$\mathrm{5}+{r}_{\mathrm{1}} =\mathrm{5}\sqrt{\mathrm{5}}\: \\ $$$${r}_{\mathrm{1}} =\mathrm{5}\sqrt{\mathrm{5}}\:−\mathrm{5}=\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right) \\ $$$$\bullet{let}\:{r}_{\mathrm{2}} \:{is}\:{radius}\:{of}\:{smaller}\:{quarter}\:{circle} \\ $$$$\:\:{r}_{\mathrm{2}} =\mathrm{10}−\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)=\mathrm{15}−\mathrm{5}\sqrt{\mathrm{5}}\: \\ $$$$\bullet{Semi}-{circle}-{area}=\frac{\pi\left(\mathrm{5}\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{25}\pi}{\mathrm{2}} \\ $$$$\bullet{Greater}-{quarter}-{circle}-{area}=\frac{\pi\left(\:\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)\:\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\bullet{Smaller}-{quarter}-{circle}-{area}=\frac{\pi\left(\:\mathrm{15}−\mathrm{5}\sqrt{\mathrm{5}}\:\:\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$${Blue}-{area}=\left({Square}-{area}\right)−\left({Semi}-{circle}-{area}+{Greater}-{quarter}-{circle}-{area}+{Smaller}-{quarter}-{circle}-{area}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{10}^{\mathrm{2}} −\left(\:\frac{\mathrm{25}\pi}{\mathrm{2}}+\frac{\pi\left(\:\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)\:\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{\pi\left(\:\mathrm{15}−\mathrm{5}\sqrt{\mathrm{5}}\:\:\right)^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{10}^{\mathrm{2}} −\left(\:\frac{\mathrm{50}}{\mathrm{4}}+\frac{\left(\:\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)\:\right)^{\mathrm{2}} }{\mathrm{4}}+\frac{\left(\:\mathrm{15}−\mathrm{5}\sqrt{\mathrm{5}}\:\:\right)^{\mathrm{2}} }{\mathrm{4}}\right)\pi \\ $$
