
Question Number 201906 by sonukgindia last updated on 15/Dec/23
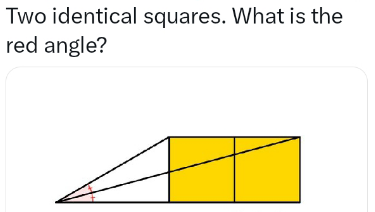
Answered by deleteduser1 last updated on 15/Dec/23
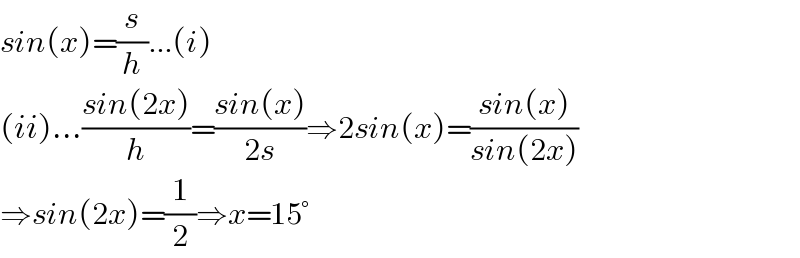
$${sin}\left({x}\right)=\frac{{s}}{{h}}...\left({i}\right) \\ $$$$\left({ii}\right)...\frac{{sin}\left(\mathrm{2}{x}\right)}{{h}}=\frac{{sin}\left({x}\right)}{\mathrm{2}{s}}\Rightarrow\mathrm{2}{sin}\left({x}\right)=\frac{{sin}\left({x}\right)}{{sin}\left(\mathrm{2}{x}\right)} \\ $$$$\Rightarrow{sin}\left(\mathrm{2}{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{x}=\mathrm{15}° \\ $$
Answered by mr W last updated on 16/Dec/23
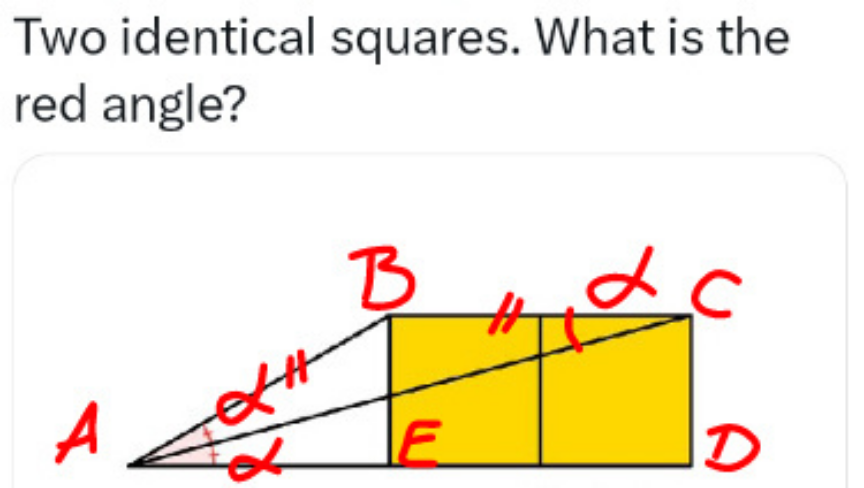
Commented by mr W last updated on 16/Dec/23
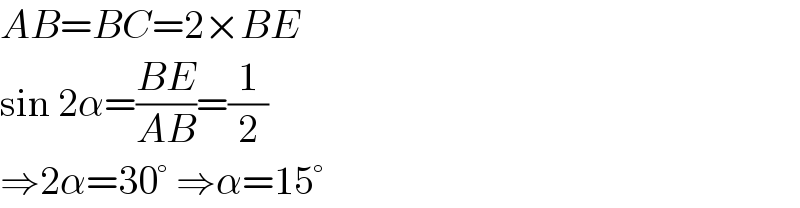
$${AB}={BC}=\mathrm{2}×{BE} \\ $$$$\mathrm{sin}\:\mathrm{2}\alpha=\frac{{BE}}{{AB}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\alpha=\mathrm{30}°\:\Rightarrow\alpha=\mathrm{15}° \\ $$
