Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

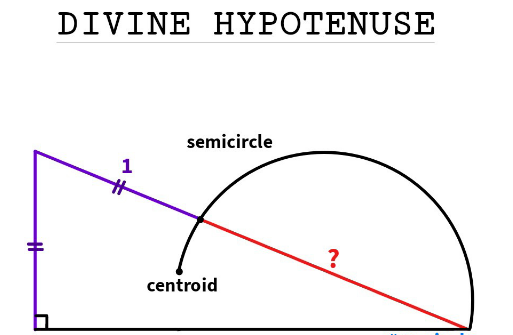
Question Number 201793 by sonukgindia last updated on 12/Dec/23

Answered by mr W last updated on 12/Dec/23

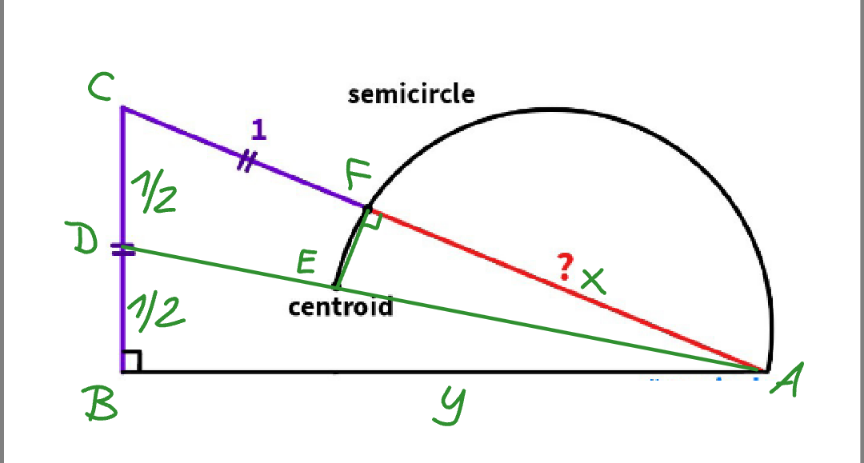
Commented by mr W last updated on 12/Dec/23

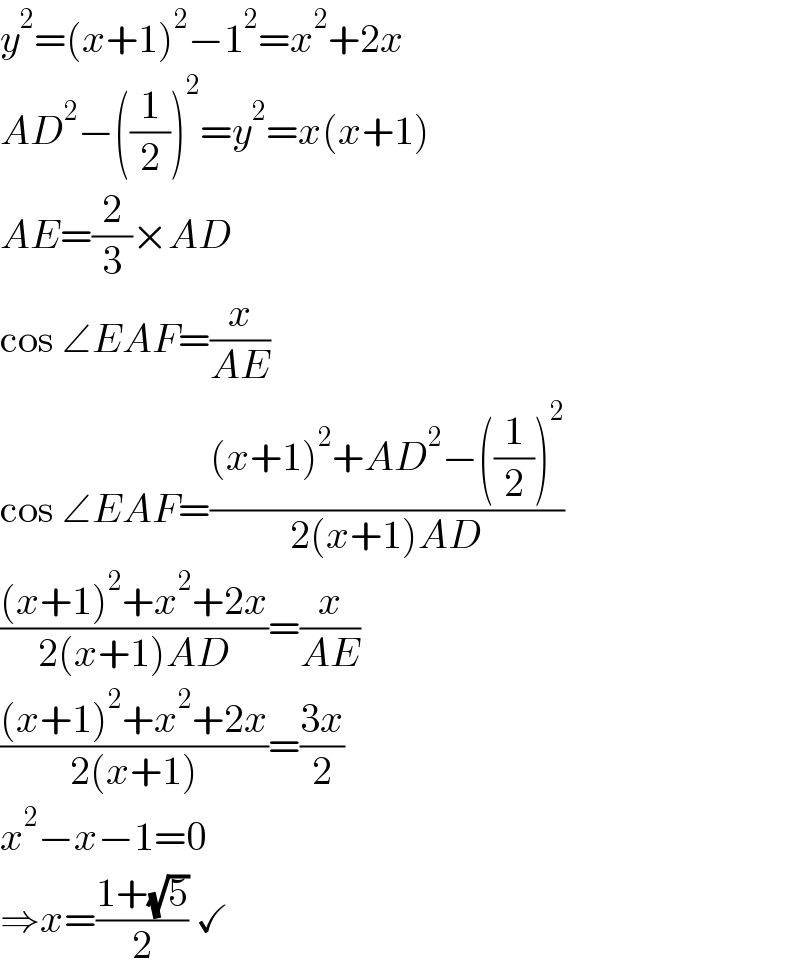
y^2 =(x+1)^2 −1^2 =x^2 +2x AD^2 −((1/2))^2 =y^2 =x(x+1) AE=(2/3)×AD cos ∠EAF=(x/(AE)) cos ∠EAF=(((x+1)^2 +AD^2 −((1/2))^2 )/(2(x+1)AD)) (((x+1)^2 +x^2 +2x)/(2(x+1)AD))=(x/(AE)) (((x+1)^2 +x^2 +2x)/(2(x+1)))=((3x)/2) x^2 −x−1=0 ⇒x=((1+(√5))/2) ✓

$${y}^{\mathrm{2}} =\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{2}{x} \\ $$$${AD}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ={y}^{\mathrm{2}} ={x}\left({x}+\mathrm{1}\right) \\ $$$${AE}=\frac{\mathrm{2}}{\mathrm{3}}×{AD} \\ $$$$\mathrm{cos}\:\angle{EAF}=\frac{{x}}{{AE}} \\ $$$$\mathrm{cos}\:\angle{EAF}=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{AD}^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}\left({x}+\mathrm{1}\right){AD}} \\ $$$$\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}{x}}{\mathrm{2}\left({x}+\mathrm{1}\right){AD}}=\frac{{x}}{{AE}} \\ $$$$\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}{x}}{\mathrm{2}\left({x}+\mathrm{1}\right)}=\frac{\mathrm{3}{x}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com