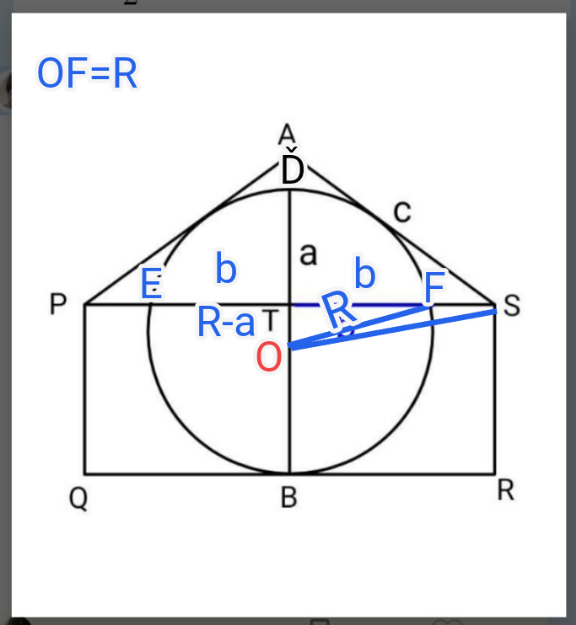
Question Number 201790 by ajfour last updated on 12/Dec/23
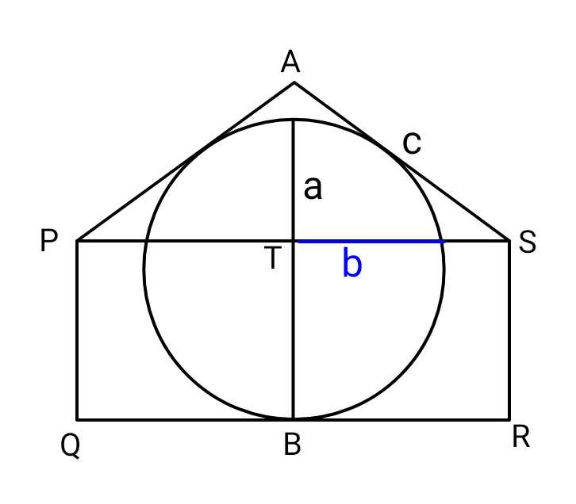
Commented by ajfour last updated on 12/Dec/23
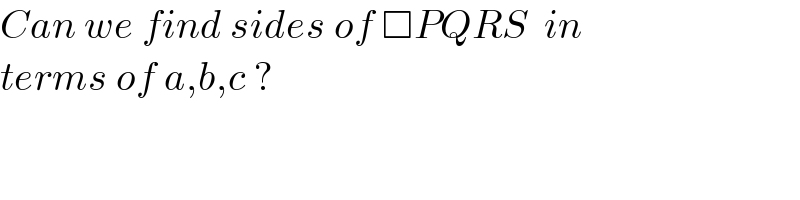
$${Can}\:{we}\:{find}\:{sides}\:{of}\:\Box{PQRS}\:\:{in} \\ $$$${terms}\:{of}\:{a},{b},{c}\:? \\ $$
Answered by a.lgnaoui last updated on 14/Dec/23
![(R−a)^2 +b^2 =R^2 ⇒ R=((a^2 +b^2 )/(2a)) BD=2R=DT+TB ⇒ TB=2R−a alors PQ =SR=(((a^2 +b^2 )/a)−a)=(b^2 /a) FS=TS−b ET=TF=b ΔOTF/OTS ∡FOT=𝛉 ∡SOT=𝛌 OF=R OS^3 =(b+FS)^2 +(R−a)^2 Posons FS=x OS^2 =(b+x)^2 +(((b^2 −a^2 ))/(4a^2 )) OS=((4a^2 (b+x)^2 +b^2 −a^2 )/(4a^2 )) cos 𝛉=(((b^2 −a^2 ))/(a^2 +b^2 )) sin 𝛉=((2ab)/(a^2 +b^2 )) cos 𝛌=(((b^2 −a^2 ))/( (√(4a^2 (b+x)+b^2 −a^2 )))) sin 𝛌=((2a(b+x))/( (√(4a^2 (b+x)+b^2 −a^2 )))) OF×OS=(((a^2 +b^2 ))/(4a^2 )) ((√(4a^2 (x+b)^2 +b^2 −a^2 ))/) ΔOFS FS^2 =OF^2 +OS^2 −2(OF×OS)cos (𝛌−𝛉) cos (𝛌−𝛉)=(((b^2 −a^2 )^2 )/( (a^2 +b^2 )(√(4a^2 (b+x)+b^2 −a^2 )))) +((4a^2 b(b+x))/((a^2 +b^2 )(√(4a^2 (b+x)+b^2 −a^2 )))) = x^2 =(((a^2 +b^2 )^2 )/(4a^2 ))+((4a^2 (b+x)^2 +b^2 −a^2 )/(4a^2 )) −2[(((a^3 +b^2 ))/(2a))×((√(4a^2 (b+x)^2 +b^2 −a^2 ))/(2a))]× (((b^2 −a^2 )^2 +4a^2 b(b+x))/((a^2 +b^2 )(√(4a^2 +(b+x)^2 +b^2 −a^2 )))) x^2 = ((a^2 +b^2 +4a^2 (b+x)^2 +b^2 −a^2 )/(4a^2 )) −(((b^2 −a^2 )^2 )/(2a^2 ))−2b(b+x) 0=((a^2 +b^2 )/(4a^2 ))+(b+x)^2 +((b^2 −a^2 )/(4a^2 ))−(((b^2 −a^2 )^2 )/(2a^2 )) −2b(b+x) x=FS ⇒ TS=b+x=X X^2 −2bX+((b^2 −(b^2 −a^2 )^2 )/(2a^2 ))=0 Δ′ =b^2 +(((b^2 −a^2 )^2 −b^2 )/(2a^2 )) =((b^4 +a^4 −2a^2 b^2 −b^2 )/(2a^2 )) X=b±(1/a)(√((a^4 +b^4 −b^2 (2a^2 +1))/2)) alors TS=b+(1/a)(√((a^4 +b^4 −b^2 (2a^2 +1))/2)) de meme pour PT cas (PE=FS) On a alors PS=PT+TS Conclusion: PS=QR=2b+(2/a)(√((a^4 +b^4 −b^2 (2a^2 +1))/2)) PQ=SR= (b^2 /a)](Q201843.png)
$$\left(\boldsymbol{\mathrm{R}}−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \:\:\Rightarrow\:\:\:\:\boldsymbol{\mathrm{R}}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}} \\ $$$$\boldsymbol{\mathrm{BD}}=\mathrm{2}\boldsymbol{\mathrm{R}}=\boldsymbol{\mathrm{DT}}+\boldsymbol{\mathrm{TB}}\:\Rightarrow\:\:\:\:\boldsymbol{\mathrm{TB}}=\mathrm{2}\boldsymbol{\mathrm{R}}−\mathrm{a} \\ $$$$\mathrm{alors}\:\:\:\boldsymbol{\mathrm{PQ}}\:\:=\boldsymbol{\mathrm{SR}}=\left(\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}}−\boldsymbol{\mathrm{a}}\right)=\frac{\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}} \\ $$$$\boldsymbol{\mathrm{FS}}=\boldsymbol{\mathrm{TS}}−\boldsymbol{\mathrm{b}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{ET}}=\boldsymbol{\mathrm{TF}}=\boldsymbol{\mathrm{b}} \\ $$$$ \\ $$$$\Delta\boldsymbol{\mathrm{OTF}}/\boldsymbol{\mathrm{OTS}}\:\:\measuredangle\boldsymbol{\mathrm{FOT}}=\boldsymbol{\theta}\:\:\:\measuredangle\boldsymbol{\mathrm{SOT}}=\boldsymbol{\lambda} \\ $$$$\:\:\boldsymbol{\mathrm{OF}}=\boldsymbol{\mathrm{R}}\:\:\:\:\boldsymbol{\mathrm{OS}}^{\mathrm{3}} =\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{FS}}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{R}}−\boldsymbol{\mathrm{a}}\right)^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{Posons}}\:\:\boldsymbol{\mathrm{FS}}=\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{OS}}^{\mathrm{2}} =\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)}{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\boldsymbol{\mathrm{OS}}=\frac{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\mathrm{cos}\:\boldsymbol{\theta}=\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }\:\:\:\:\:\:\mathrm{sin}\:\boldsymbol{\theta}=\frac{\mathrm{2}\boldsymbol{\mathrm{ab}}}{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{cos}\:\boldsymbol{\lambda}=\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }} \\ $$$$\mathrm{sin}\:\boldsymbol{\lambda}=\frac{\mathrm{2}\boldsymbol{\mathrm{a}}\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)}{\:\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }} \\ $$$$\boldsymbol{\mathrm{OF}}×\boldsymbol{\mathrm{OS}}=\frac{\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{b}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}{} \\ $$$$ \\ $$$$\Delta\boldsymbol{\mathrm{OFS}} \\ $$$$\:\:\boldsymbol{\mathrm{FS}}^{\mathrm{2}} =\boldsymbol{\mathrm{OF}}^{\mathrm{2}} +\boldsymbol{\mathrm{OS}}^{\mathrm{2}} −\mathrm{2}\left(\boldsymbol{\mathrm{OF}}×\boldsymbol{\mathrm{OS}}\right)\mathrm{cos}\:\left(\boldsymbol{\lambda}−\boldsymbol{\theta}\right) \\ $$$$\mathrm{cos}\:\left(\boldsymbol{\lambda}−\boldsymbol{\theta}\right)=\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\:\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:+\frac{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)}{\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }} \\ $$$$= \\ $$$$ \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\frac{\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }+\frac{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:−\mathrm{2}\left[\frac{\left(\boldsymbol{\mathrm{a}}^{\mathrm{3}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)}{\mathrm{2}\boldsymbol{\mathrm{a}}}×\frac{\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}{\mathrm{2}\boldsymbol{\mathrm{a}}}\right]× \\ $$$$\:\:\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)}{\left(\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} \right)\sqrt{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\:\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:\:−\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }−\mathrm{2}\boldsymbol{\mathrm{b}}\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right) \\ $$$$\mathrm{0}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }+\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right)^{\mathrm{2}} +\frac{\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{4}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }−\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:−\mathrm{2}\boldsymbol{\mathrm{b}}\left(\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}\right) \\ $$$$\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{FS}}\:\:\:\:\Rightarrow\:\:\:\mathrm{T}\boldsymbol{\mathrm{S}}=\boldsymbol{\mathrm{b}}+\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{X}} \\ $$$$\boldsymbol{\mathrm{X}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{bX}}+\frac{\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Delta'\:\:=\boldsymbol{\mathrm{b}}^{\mathrm{2}} +\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\frac{\boldsymbol{\mathrm{b}}^{\mathrm{4}} +\boldsymbol{\mathrm{a}}^{\mathrm{4}} −\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} \boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\:\:\:\boldsymbol{\mathrm{X}}=\boldsymbol{\mathrm{b}}\pm\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}}\sqrt{\frac{\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\boldsymbol{\mathrm{b}}^{\mathrm{4}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\boldsymbol{\mathrm{alors}}\:\:\boldsymbol{\mathrm{TS}}=\boldsymbol{\mathrm{b}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}}\sqrt{\frac{\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\boldsymbol{\mathrm{b}}^{\mathrm{4}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$ \\ $$$$\:\:\:\:\boldsymbol{\mathrm{de}}\:\boldsymbol{\mathrm{meme}}\:\boldsymbol{\mathrm{pour}}\:\boldsymbol{\mathrm{PT}}\:\boldsymbol{\mathrm{cas}}\:\:\left(\boldsymbol{\mathrm{PE}}=\boldsymbol{\mathrm{FS}}\right) \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{On}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{alors}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{PS}}=\boldsymbol{\mathrm{PT}}+\boldsymbol{\mathrm{TS}} \\ $$$$\boldsymbol{{Conclusion}}: \\ $$$$ \\ $$$$\:\boldsymbol{\mathrm{PS}}=\boldsymbol{\mathrm{QR}}=\mathrm{2}\boldsymbol{\mathrm{b}}+\frac{\mathrm{2}}{\boldsymbol{\mathrm{a}}}\sqrt{\frac{\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\boldsymbol{\mathrm{b}}^{\mathrm{4}} −\boldsymbol{\mathrm{b}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$\:\boldsymbol{\mathrm{PQ}}=\boldsymbol{\mathrm{SR}}=\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{\mathrm{b}}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 14/Dec/23