
Question Number 201604 by ajfour last updated on 09/Dec/23
Commented by ajfour last updated on 09/Dec/23
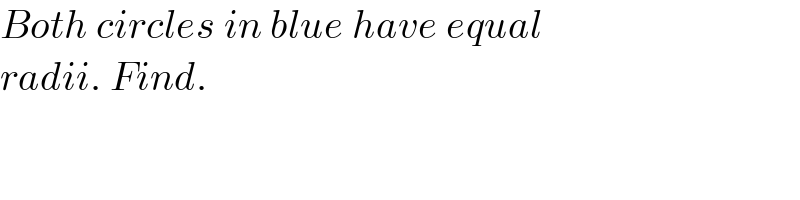
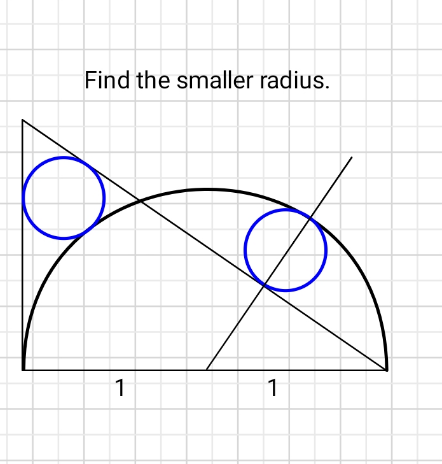
$${Both}\:{circles}\:{in}\:{blue}\:{have}\:{equal} \\ $$$${radii}.\:{Find}. \\ $$
Answered by mr W last updated on 09/Dec/23
Commented by mr W last updated on 09/Dec/23

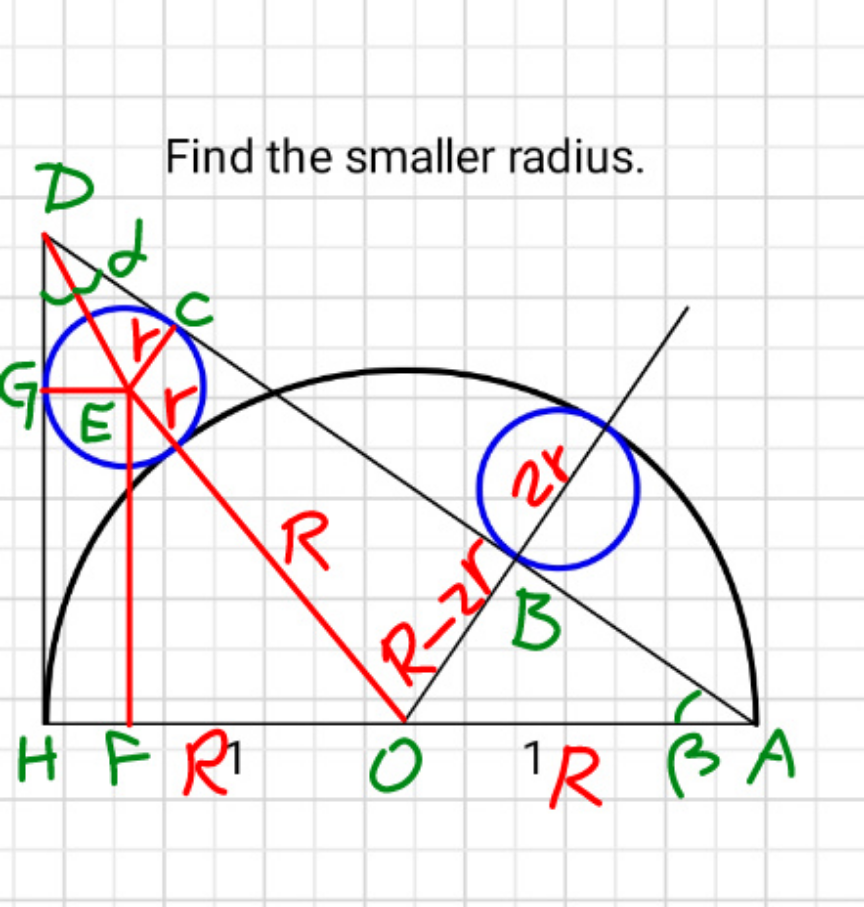
$$\lambda=\frac{{r}}{{R}} \\ $$$$\mathrm{sin}\:\beta=\frac{{R}−\mathrm{2}{r}}{{R}}=\mathrm{1}−\mathrm{2}\lambda \\ $$$$\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{sin}\:\beta}{\mathrm{1}+\mathrm{cos}\:\beta}=\frac{\mathrm{1}−\mathrm{2}\lambda}{\mathrm{1}+\mathrm{2}\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}} \\ $$$$\alpha=\frac{\frac{\pi}{\mathrm{2}}−\beta}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}−\frac{\beta}{\mathrm{2}} \\ $$$${DC}={DG}=\frac{{r}}{\mathrm{tan}\:\alpha}=\frac{{r}\left(\mathrm{1}+\mathrm{tan}\:\frac{\beta}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\:\frac{\beta}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:=\frac{{r}\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{2}\lambda}{\mathrm{1}+\mathrm{2}\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}}\right)}{\mathrm{1}−\frac{\mathrm{1}−\mathrm{2}\lambda}{\mathrm{1}+\mathrm{2}\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}}}=\frac{{r}\left(\mathrm{1}−\lambda+\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}+\lambda} \\ $$$${EF}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{Rr}} \\ $$$${DH}=\frac{{r}\left(\mathrm{1}−\lambda+\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}+\lambda}+\mathrm{2}\sqrt{{Rr}} \\ $$$${DH}=\mathrm{2}{R}\:\mathrm{tan}\:\beta=\frac{\mathrm{2}{R}\left(\mathrm{1}−\mathrm{2}\lambda\right)}{\mathrm{2}\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}}=\frac{{R}\left(\mathrm{1}−\mathrm{2}\lambda\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}} \\ $$$$\frac{{r}\left(\mathrm{1}−\lambda+\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}+\lambda}+\mathrm{2}\sqrt{{Rr}}=\frac{{R}\left(\mathrm{1}−\mathrm{2}\lambda\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}} \\ $$$$\frac{\lambda\left(\mathrm{1}−\lambda+\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}\right)}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}+\lambda}+\mathrm{2}\sqrt{\lambda}=\frac{\mathrm{1}−\mathrm{2}\lambda}{\:\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}} \\ $$$$\Rightarrow\lambda\approx\mathrm{0}.\mathrm{21995157} \\ $$
Commented by ajfour last updated on 09/Dec/23
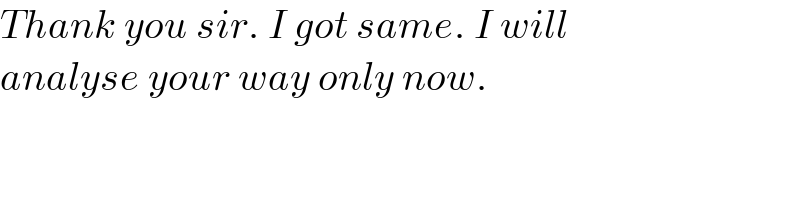
$${Thank}\:{you}\:{sir}.\:{I}\:{got}\:{same}.\:{I}\:{will} \\ $$$${analyse}\:{your}\:{way}\:{only}\:{now}. \\ $$
Answered by ajfour last updated on 09/Dec/23
Commented by ajfour last updated on 09/Dec/23
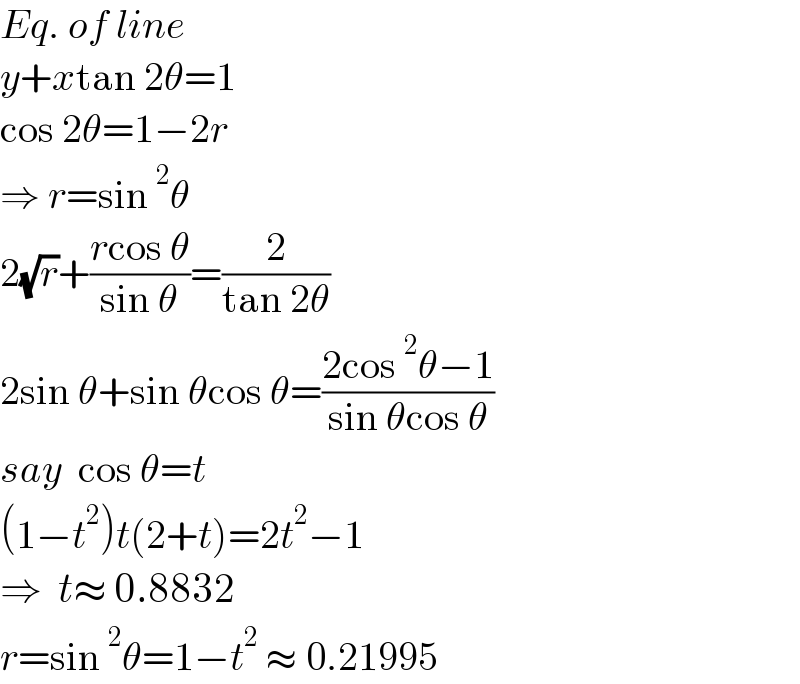
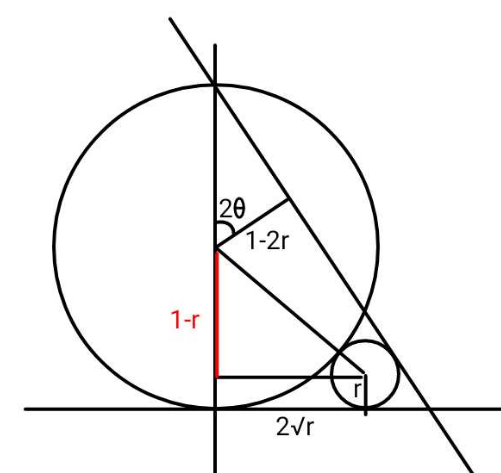
$${Eq}.\:{of}\:{line} \\ $$$${y}+{x}\mathrm{tan}\:\mathrm{2}\theta=\mathrm{1} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta=\mathrm{1}−\mathrm{2}{r} \\ $$$$\Rightarrow\:{r}=\mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$$\mathrm{2}\sqrt{{r}}+\frac{{r}\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}=\frac{\mathrm{2}}{\mathrm{tan}\:\mathrm{2}\theta} \\ $$$$\mathrm{2sin}\:\theta+\mathrm{sin}\:\theta\mathrm{cos}\:\theta=\frac{\mathrm{2cos}\:^{\mathrm{2}} \theta−\mathrm{1}}{\mathrm{sin}\:\theta\mathrm{cos}\:\theta} \\ $$$${say}\:\:\mathrm{cos}\:\theta={t} \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right){t}\left(\mathrm{2}+{t}\right)=\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:\:{t}\approx\:\mathrm{0}.\mathrm{8832} \\ $$$${r}=\mathrm{sin}\:^{\mathrm{2}} \theta=\mathrm{1}−{t}^{\mathrm{2}} \:\approx\:\mathrm{0}.\mathrm{21995} \\ $$
Commented by mr W last updated on 09/Dec/23

$${nice}\:{solution}! \\ $$
Commented by Frix last updated on 10/Dec/23
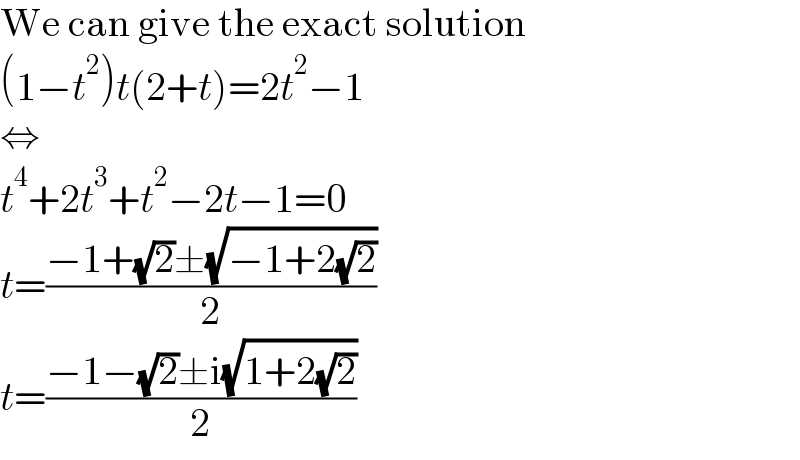
$$\mathrm{We}\:\mathrm{can}\:\mathrm{give}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{solution} \\ $$$$\left(\mathrm{1}−{t}^{\mathrm{2}} \right){t}\left(\mathrm{2}+{t}\right)=\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Leftrightarrow \\ $$$${t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{−\mathrm{1}+\sqrt{\mathrm{2}}\pm\sqrt{−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$${t}=\frac{−\mathrm{1}−\sqrt{\mathrm{2}}\pm\mathrm{i}\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 28/Oct/24
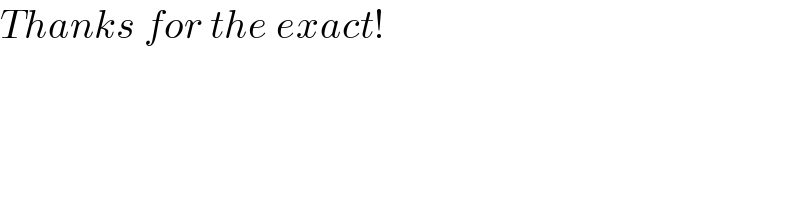
$${Thanks}\:{for}\:{the}\:{exact}! \\ $$
