Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 201329 by MrGHK last updated on 04/Dec/23

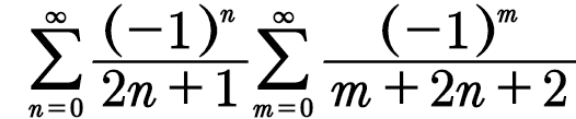
Answered by witcher3 last updated on 04/Dec/23

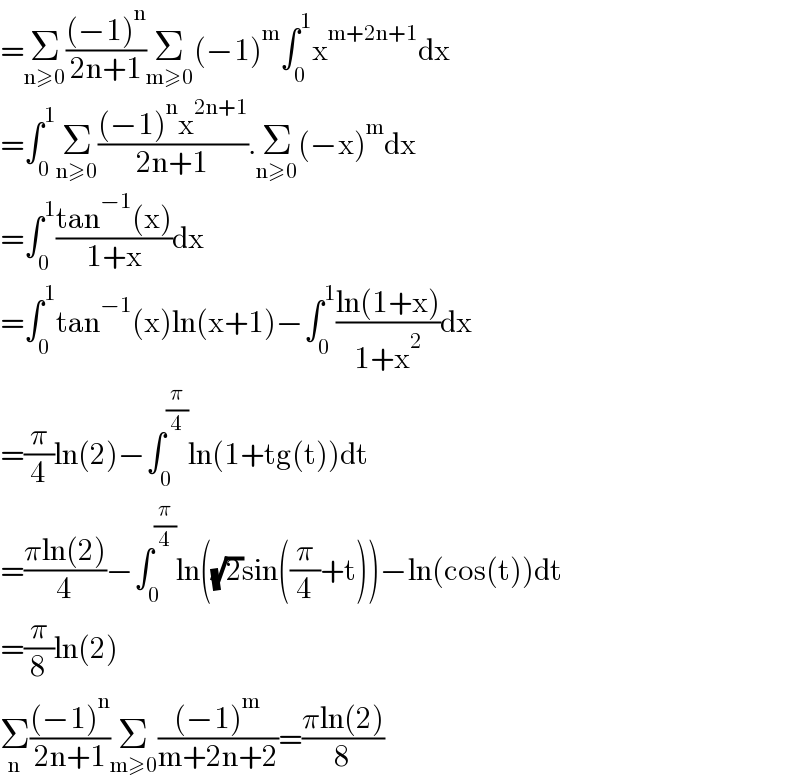
=Σ_(n≥0) (((−1)^n )/(2n+1))Σ_(m≥0) (−1)^m ∫_0 ^1 x^(m+2n+1) dx =∫_0 ^1 Σ_(n≥0) (((−1)^n x^(2n+1) )/(2n+1)).Σ_(n≥0) (−x)^m dx =∫_0 ^1 ((tan^(−1) (x))/(1+x))dx =∫_0 ^1 tan^(−1) (x)ln(x+1)−∫_0 ^1 ((ln(1+x))/(1+x^2 ))dx =(π/4)ln(2)−∫_0 ^(π/4) ln(1+tg(t))dt =((πln(2))/4)−∫_0 ^(π/4) ln((√2)sin((π/4)+t))−ln(cos(t))dt =(π/8)ln(2) Σ_n (((−1)^n )/(2n+1))Σ_(m≥0) (((−1)^m )/(m+2n+2))=((πln(2))/8)

$$=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\underset{\mathrm{m}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{\mathrm{m}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{m}+\mathrm{2n}+\mathrm{1}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}.\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{x}\right)^{\mathrm{m}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{tg}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}+\mathrm{t}\right)\right)−\mathrm{ln}\left(\mathrm{cos}\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$=\frac{\pi}{\mathrm{8}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\underset{\mathrm{n}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}+\mathrm{1}}\underset{\mathrm{m}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{m}} }{\mathrm{m}+\mathrm{2n}+\mathrm{2}}=\frac{\pi\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$

Commented by MrGHK last updated on 05/Dec/23

wonderful

$${wonderful} \\ $$

Commented by witcher3 last updated on 05/Dec/23

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com