
Question Number 201325 by sonukgindia last updated on 04/Dec/23
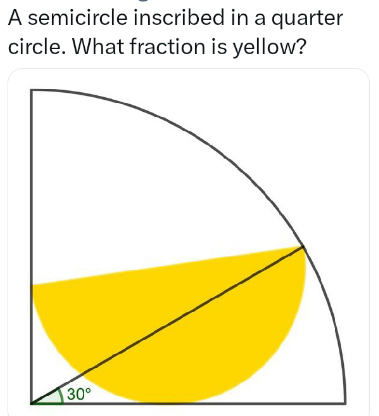
Commented by mr W last updated on 05/Dec/23
$${do}\:{you}\:{have}\:{the}\:{right}\:{answer}? \\ $$
Answered by mr W last updated on 04/Dec/23
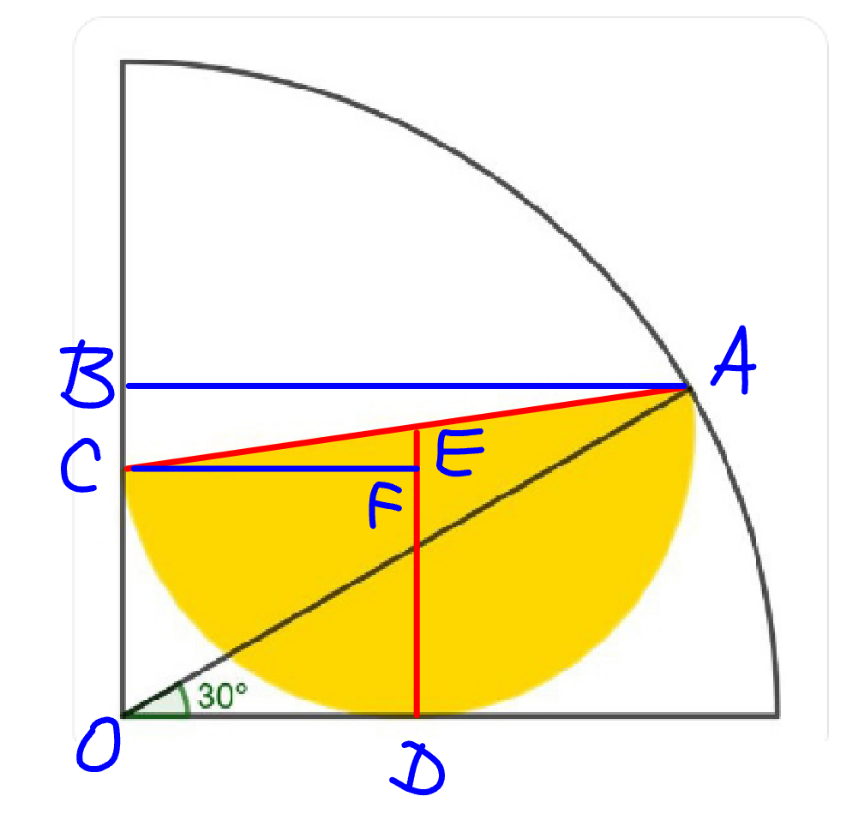
Commented by mr W last updated on 04/Dec/23

$${R}={radius}\:{of}\:{big}\:{quarter}\:{circle} \\ $$$${r}={radius}\:{of}\:{small}\:{semi}\:\:{circle} \\ $$$${OB}=\frac{{R}}{\mathrm{2}} \\ $$$${AB}=\frac{\sqrt{\mathrm{3}}{R}}{\mathrm{2}} \\ $$$${BC}=\sqrt{\left(\mathrm{2}{r}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{R}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${CO}=\frac{{R}}{\mathrm{2}}−\sqrt{\left(\mathrm{2}{r}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{R}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${EF}={r}−\frac{{R}}{\mathrm{2}}+\sqrt{\left(\mathrm{2}{r}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{R}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{{BC}}{\mathrm{2}} \\ $$$$\mathrm{2}\left(\frac{{R}}{\mathrm{2}}−{r}\right)=\sqrt{\left(\mathrm{2}{r}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{3}}{R}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{4}\left(\frac{{R}^{\mathrm{2}} }{\mathrm{4}}−{Rr}+{r}^{\mathrm{2}} \right)=\mathrm{4}{r}^{\mathrm{2}} −\frac{\mathrm{3}{R}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{7}{R}}{\mathrm{16}} \\ $$$$\frac{{semi}}{{quarter}}=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{4}}{\pi{R}^{\mathrm{2}} }=\mathrm{2}\left(\frac{{r}}{{R}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\frac{\mathrm{7}}{\mathrm{16}}\right)^{\mathrm{2}} =\frac{\mathrm{49}}{\mathrm{128}}\approx\mathrm{38}.\mathrm{2\%} \\ $$
