
Question Number 201322 by cherokeesay last updated on 04/Dec/23
Answered by mr W last updated on 05/Dec/23
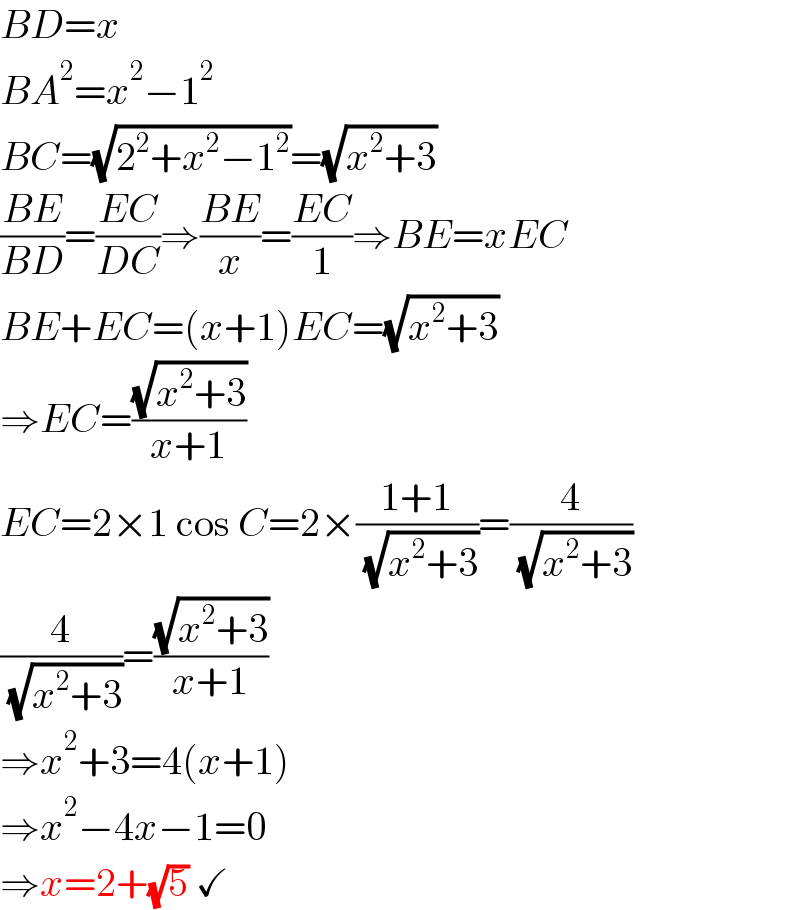
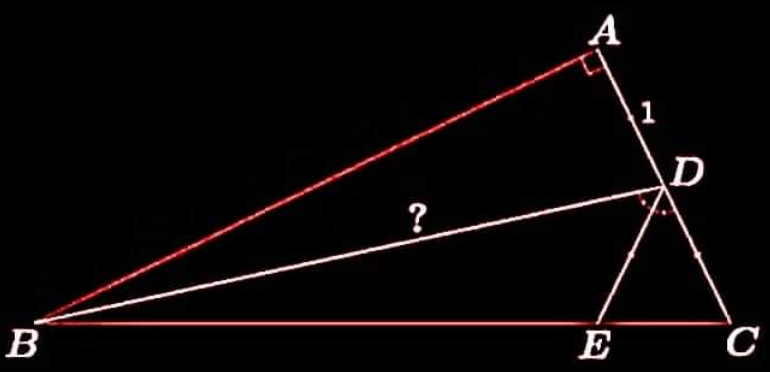
$${BD}={x} \\ $$$${BA}^{\mathrm{2}} ={x}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \\ $$$${BC}=\sqrt{\mathrm{2}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\frac{{BE}}{{BD}}=\frac{{EC}}{{DC}}\Rightarrow\frac{{BE}}{{x}}=\frac{{EC}}{\mathrm{1}}\Rightarrow{BE}={xEC} \\ $$$${BE}+{EC}=\left({x}+\mathrm{1}\right){EC}=\sqrt{{x}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\Rightarrow{EC}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{{x}+\mathrm{1}} \\ $$$${EC}=\mathrm{2}×\mathrm{1}\:\mathrm{cos}\:{C}=\mathrm{2}×\frac{\mathrm{1}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}=\frac{\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}} \\ $$$$\frac{\mathrm{4}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{3}=\mathrm{4}\left({x}+\mathrm{1}\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{2}+\sqrt{\mathrm{5}}\:\checkmark \\ $$
Commented by cherokeesay last updated on 05/Dec/23

$${thank}\:{you}\:{sir}\:! \\ $$
