
Question Number 201298 by ajfour last updated on 03/Dec/23
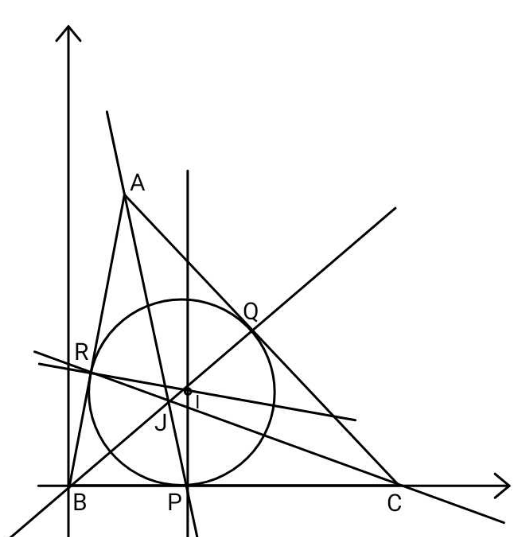
Commented by ajfour last updated on 03/Dec/23
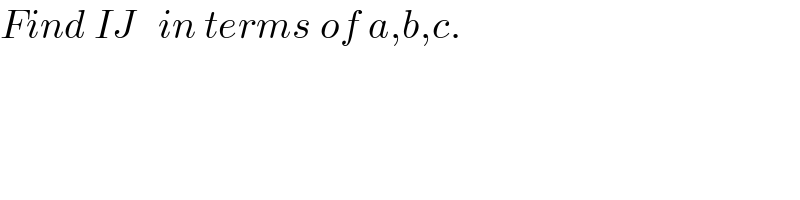
$${Find}\:{IJ}\:\:\:{in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by mr W last updated on 05/Jan/24
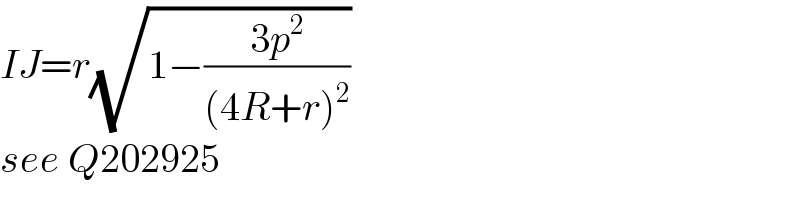
$${IJ}={r}\sqrt{\mathrm{1}−\frac{\mathrm{3}{p}^{\mathrm{2}} }{\left(\mathrm{4}{R}+{r}\right)^{\mathrm{2}} }} \\ $$$${see}\:{Q}\mathrm{202925} \\ $$
Answered by ajfour last updated on 03/Dec/23
![BC=ai BA=c^� =hi+kj BI=rcot (β/2)i+rj BR=rcot (β/2)(((hi+kj)/( (√(h^2 +k^2 ))))) eq. of JC r_J ^� =ai+ λ{(a−((rh)/( (√(h^2 +k^2 ))))cot (β/2))i−(((rk)/( (√(h^2 +k^2 )))))j} eq. of JA r_J ^� =(hi+kj)+μ{(rcot (β/2)−h)i−kj} r_J ^� =r_J ^� a+λ(a−((rh)/( (√(h^2 +k^2 ))))cot (β/2)) =h+μ(rcot (β/2)−h) & ((λr)/( (√(h^2 +k^2 ))))=μ−1 ⇒ a+λ(a−((rh)/( (√(h^2 +k^2 ))))cot (β/2)) =h+(1+((λr)/( (√(h^2 +k^2 )))))(rcot (β/2)−h) ⇒ λ=((a−h−(rcot (β/2)−h))/((r^2 /( (√(h^2 +k^2 ))))cot (β/2)−a)) IJ=[a+{((a−h−(rcot (β/2)−h))/((r^2 /( (√(h^2 +k^2 ))))cot (β/2)−a))}{(a−((rh)/( (√(h^2 +k^2 ))))cot (β/2))−rcot (β/2)}]i +[{((a−h−(rcot (β/2)−h))/((r^2 /( (√(h^2 +k^2 ))))cot (β/2)−a))}(r/( (√(h^2 +k^2 ))))−r]j h=ccos β and k=csin β ⇒ IJ=[a+{((a−ccos β−(rcot (β/2)−ccos β))/((r^2 /c)cot (β/2)−a))}{(a−rcos βcot (β/2))−rcot (β/2)}]i +[{((a−ccos β−(rcot (β/2)−ccos β))/((r^2 /c)cot (β/2)−a))}(r/c)−r]j r=((2△)/(a+b+c))](Q201301.png)
$${BC}={ai} \\ $$$${BA}=\bar {{c}}={hi}+{kj} \\ $$$${BI}={r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}{i}+{rj} \\ $$$${BR}={r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\left(\frac{{hi}+{kj}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\right) \\ $$$${eq}.\:{of}\:{JC} \\ $$$$\bar {{r}}_{{J}} ={ai}+ \\ $$$$\lambda\left\{\left({a}−\frac{{rh}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right){i}−\left(\frac{{rk}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\right){j}\right\} \\ $$$${eq}.\:{of}\:{JA} \\ $$$$\bar {{r}}_{{J}} =\left({hi}+{kj}\right)+\mu\left\{\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right){i}−{kj}\right\} \\ $$$$\bar {{r}}_{{J}} =\bar {{r}}_{{J}} \\ $$$${a}+\lambda\left({a}−\frac{{rh}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right) \\ $$$$\:\:={h}+\mu\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right) \\ $$$$\&\:\:\frac{\lambda{r}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}=\mu−\mathrm{1} \\ $$$$\Rightarrow\:{a}+\lambda\left({a}−\frac{{rh}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right) \\ $$$$\:\:\:\:={h}+\left(\mathrm{1}+\frac{\lambda{r}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\right)\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right) \\ $$$$\Rightarrow\:\lambda=\frac{{a}−{h}−\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right)}{\frac{{r}^{\mathrm{2}} }{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{a}} \\ $$$${IJ}=\left[{a}+\left\{\frac{{a}−{h}−\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right)}{\frac{{r}^{\mathrm{2}} }{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{a}}\right\}\left\{\left({a}−\frac{{rh}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right)−{r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right\}\right]{i} \\ $$$$\:\:\:\:+\left[\left\{\frac{{a}−{h}−\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{h}\right)}{\frac{{r}^{\mathrm{2}} }{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{a}}\right\}\frac{{r}}{\:\sqrt{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} }}−{r}\right]{j} \\ $$$${h}={c}\mathrm{cos}\:\beta\:\:\:\:{and}\:\:\:{k}={c}\mathrm{sin}\:\beta \\ $$$$\Rightarrow \\ $$$${IJ}=\left[{a}+\left\{\frac{{a}−{c}\mathrm{cos}\:\beta−\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{c}\mathrm{cos}\:\beta\right)}{\frac{{r}^{\mathrm{2}} }{{c}}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{a}}\right\}\left\{\left({a}−{r}\mathrm{cos}\:\beta\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right)−{r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}\right\}\right]{i} \\ $$$$\:\:\:\:+\left[\left\{\frac{{a}−{c}\mathrm{cos}\:\beta−\left({r}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{c}\mathrm{cos}\:\beta\right)}{\frac{{r}^{\mathrm{2}} }{{c}}\mathrm{cot}\:\frac{\beta}{\mathrm{2}}−{a}}\right\}\frac{{r}}{{c}}−{r}\right]{j} \\ $$$${r}=\frac{\mathrm{2}\bigtriangleup}{{a}+{b}+{c}} \\ $$
Commented by mr W last updated on 04/Dec/23

$${very}\:{nice}! \\ $$
