
Question Number 201292 by sonukgindia last updated on 03/Dec/23
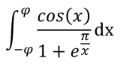
Answered by aleks041103 last updated on 03/Dec/23
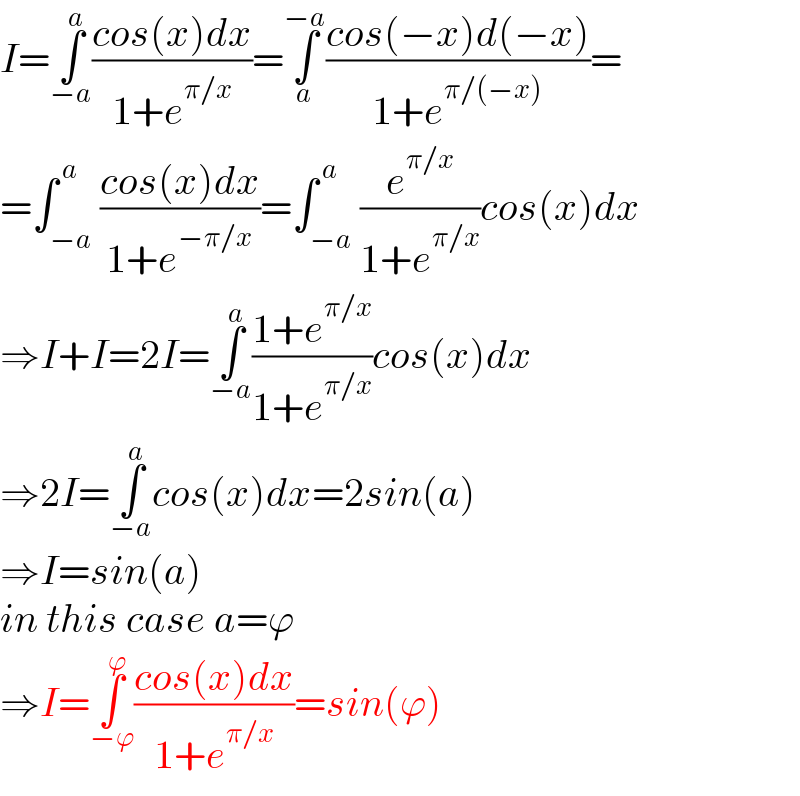
$${I}=\underset{−{a}} {\overset{{a}} {\int}}\frac{{cos}\left({x}\right){dx}}{\mathrm{1}+{e}^{\pi/{x}} }=\underset{{a}} {\overset{−{a}} {\int}}\frac{{cos}\left(−{x}\right){d}\left(−{x}\right)}{\mathrm{1}+{e}^{\pi/\left(−{x}\right)} }= \\ $$$$=\int_{−{a}} ^{\:{a}} \frac{{cos}\left({x}\right){dx}}{\mathrm{1}+{e}^{−\pi/{x}} }=\int_{−{a}} ^{\:{a}} \frac{{e}^{\pi/{x}} }{\mathrm{1}+{e}^{\pi/{x}} }{cos}\left({x}\right){dx} \\ $$$$\Rightarrow{I}+{I}=\mathrm{2}{I}=\underset{−{a}} {\overset{{a}} {\int}}\frac{\mathrm{1}+{e}^{\pi/{x}} }{\mathrm{1}+{e}^{\pi/{x}} }{cos}\left({x}\right){dx} \\ $$$$\Rightarrow\mathrm{2}{I}=\underset{−{a}} {\overset{{a}} {\int}}{cos}\left({x}\right){dx}=\mathrm{2}{sin}\left({a}\right) \\ $$$$\Rightarrow{I}={sin}\left({a}\right) \\ $$$${in}\:{this}\:{case}\:{a}=\varphi \\ $$$$\Rightarrow{I}=\underset{−\varphi} {\overset{\varphi} {\int}}\frac{{cos}\left({x}\right){dx}}{\mathrm{1}+{e}^{\pi/{x}} }={sin}\left(\varphi\right) \\ $$
