
Question Number 201289 by sonukgindia last updated on 03/Dec/23
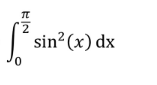
Commented by mr W last updated on 03/Dec/23

$${sir}: \\ $$$${why}\:{do}\:{you}\:{ignore}\:{all}\:{questions} \\ $$$${other}\:{people}\:{are}\:{asking}\:{you}? \\ $$
Answered by BaliramKumar last updated on 04/Dec/23
![∫_0 ^(π/2) sin^2 xdx = ∫_0 ^(π/2) (√(1−cos^2 x)) sinxdx = put cosx = t −sinxdx = dt x=(π/2) → t= 0 x=0 → t=1 −∫_1 ^0 (√(1−t^2 ))dt = ∫_0 ^1 (√(1−t^2 ))dt [(t/2)(√(1−t^2 )) + (1/2)sin^(−1) t]_0 ^1 = (π/4)](Q201317.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{xdx}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\mathrm{sinxdx}\:=\: \\ $$$$ \\ $$$$\mathrm{put}\:\:\:\:\:\mathrm{cosx}\:=\:\mathrm{t}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{sinxdx}\:=\:\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\frac{\pi}{\mathrm{2}}\:\:\:\rightarrow\:\mathrm{t}=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{0}\:\:\rightarrow\:\:\:\:\:\mathrm{t}=\mathrm{1} \\ $$$$−\int_{\mathrm{1}} ^{\mathrm{0}} \:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\: \\ $$$$\left[\frac{\mathrm{t}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} \:}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \mathrm{t}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Calculusboy last updated on 03/Dec/23
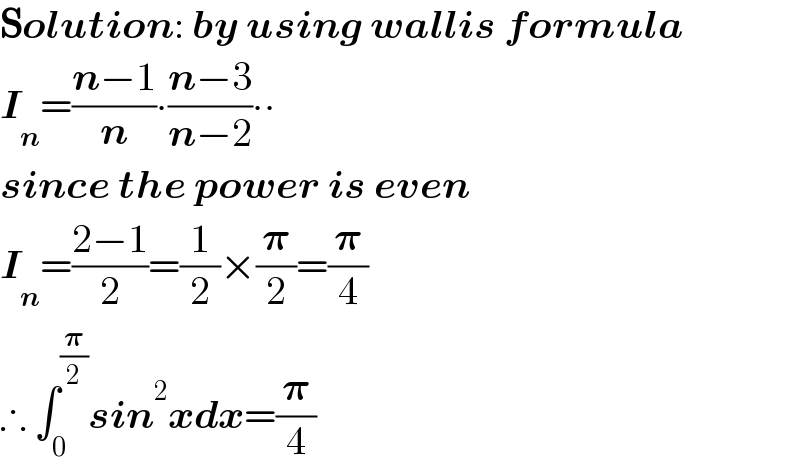
$$\boldsymbol{\mathrm{S}{olution}}:\:\boldsymbol{{by}}\:\boldsymbol{{using}}\:\boldsymbol{{wallis}}\:\boldsymbol{{formula}} \\ $$$$\boldsymbol{{I}}_{\boldsymbol{{n}}} =\frac{\boldsymbol{{n}}−\mathrm{1}}{\boldsymbol{{n}}}\centerdot\frac{\boldsymbol{{n}}−\mathrm{3}}{\boldsymbol{{n}}−\mathrm{2}}\centerdot\centerdot \\ $$$$\boldsymbol{{since}}\:\boldsymbol{{the}}\:\boldsymbol{{power}}\:\boldsymbol{{is}}\:\boldsymbol{{even}} \\ $$$$\boldsymbol{{I}}_{\boldsymbol{{n}}} =\frac{\mathrm{2}−\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\boldsymbol{\pi}}{\mathrm{2}}=\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{xdx}}=\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 04/Dec/23
![=∫_0 ^(π/2) ((1−cos 2x)/2)dx =(1/2)[x−((sin 2x)/2)]_0 ^(π/2) =(π/4)](Q201310.png)
$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}−\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\pi}{\mathrm{4}} \\ $$
