
Question Number 201184 by Calculusboy last updated on 01/Dec/23
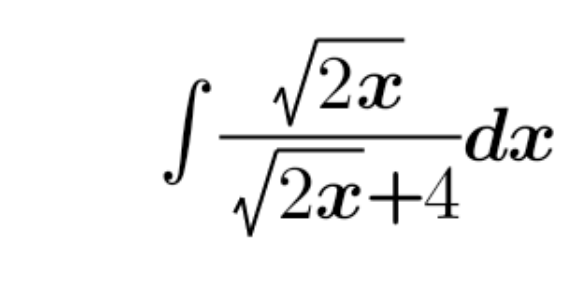
Answered by Sutrisno last updated on 01/Dec/23
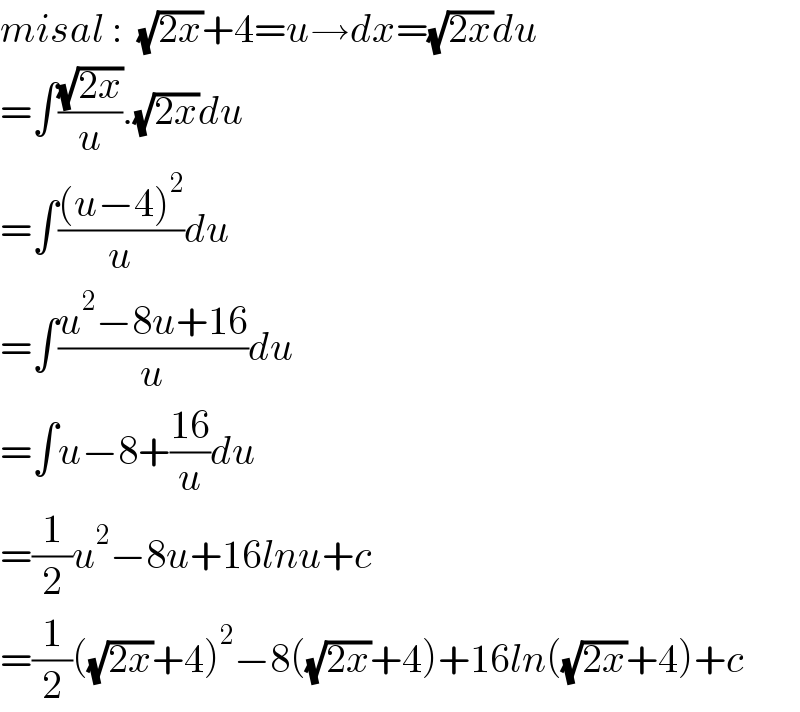
$${misal}\::\:\:\sqrt{\mathrm{2}{x}}+\mathrm{4}={u}\rightarrow{dx}=\sqrt{\mathrm{2}{x}}{du} \\ $$$$=\int\frac{\sqrt{\mathrm{2}{x}}}{{u}}.\sqrt{\mathrm{2}{x}}{du} \\ $$$$=\int\frac{\left({u}−\mathrm{4}\right)^{\mathrm{2}} }{{u}}{du} \\ $$$$=\int\frac{{u}^{\mathrm{2}} −\mathrm{8}{u}+\mathrm{16}}{{u}}{du} \\ $$$$=\int{u}−\mathrm{8}+\frac{\mathrm{16}}{{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{u}^{\mathrm{2}} −\mathrm{8}{u}+\mathrm{16}{lnu}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{2}{x}}+\mathrm{4}\right)^{\mathrm{2}} −\mathrm{8}\left(\sqrt{\mathrm{2}{x}}+\mathrm{4}\right)+\mathrm{16}{ln}\left(\sqrt{\mathrm{2}{x}}+\mathrm{4}\right)+{c} \\ $$
Commented by Calculusboy last updated on 01/Dec/23
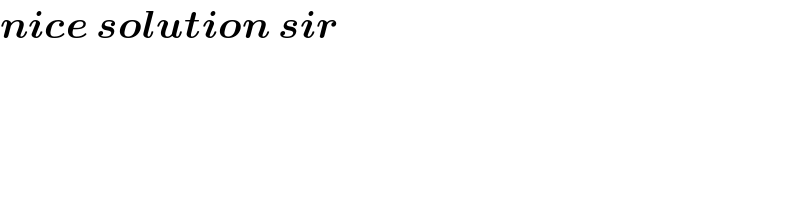
$$\boldsymbol{{nice}}\:\boldsymbol{{solution}}\:\boldsymbol{{sir}} \\ $$
