Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 201035 by sonukgindia last updated on 28/Nov/23

Commented by mr W last updated on 28/Nov/23

the side length of the square can not be equal to the radius of the smaller semi−circles!

$${the}\:{side}\:{length}\:{of}\:{the}\:{square}\:{can}\:{not} \\ $$$${be}\:{equal}\:{to}\:{the}\:{radius}\:{of}\:{the}\:{smaller} \\ $$$${semi}−{circles}! \\ $$

Commented by mr W last updated on 28/Nov/23

Answered by a.lgnaoui last updated on 29/Nov/23

Pink triangle ABC Blue triangle BDE BD=2×(R/4)=(R/2) BH=(R/4) ⇒Blue Area=((R/4)×(R/2))×(1/2)=(R^2 /(16)) (1) BC//OE BC^2 =OH^2 +BH^2 =OB^2 R^2 =OH^2 +(R^2 /4^2 ) =AB^2 +(R^2 /4) ⇒ AB=((R(√3))/2) AC=(R/2) Pink Area= (1/2) (AB×AC)=((R^2 (√3))/8) ((Pink )/(Blue))=(((R^2 (√3))/8)/(R^2 /(16)))=((R^2 (√3))/8)×((16)/R^2 ) =2(√3) X (Voir Resultat exact dessous: 3,1334)

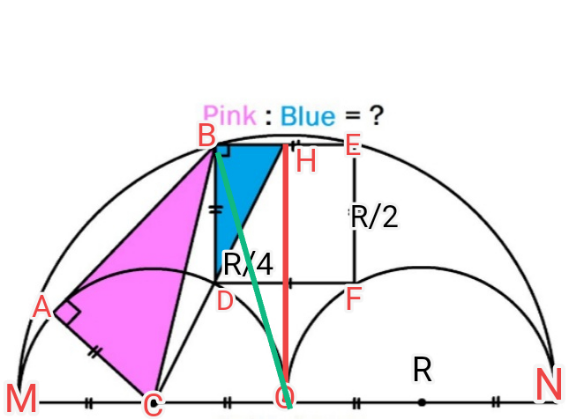
$$\boldsymbol{\mathrm{P}}\mathrm{ink}\:\mathrm{triangle}\:\:\:\:\:\:\boldsymbol{\mathrm{ABC}} \\ $$$$\boldsymbol{\mathrm{B}}\mathrm{lue}\:\mathrm{triangle}\:\:\:\:\:\:\:\boldsymbol{\mathrm{BDE}} \\ $$$$\boldsymbol{\mathrm{BD}}=\mathrm{2}×\frac{\boldsymbol{\mathrm{R}}}{\mathrm{4}}=\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{BH}}=\frac{\boldsymbol{\mathrm{R}}}{\mathrm{4}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{Blue}}\:\:\boldsymbol{\mathrm{Area}}=\left(\frac{\boldsymbol{\mathrm{R}}}{\mathrm{4}}×\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{16}}\:\:\:\left(\mathrm{1}\right) \\ $$$$\boldsymbol{\mathrm{BC}}//\boldsymbol{\mathrm{OE}}\:\:\:\:\:\:\boldsymbol{\mathrm{BC}}^{\mathrm{2}} =\boldsymbol{\mathrm{OH}}^{\mathrm{2}} +\boldsymbol{\mathrm{BH}}^{\mathrm{2}} =\boldsymbol{\mathrm{OB}}^{\mathrm{2}} \\ $$$$\:\:\boldsymbol{\mathrm{R}}^{\mathrm{2}} =\boldsymbol{\mathrm{OH}}^{\mathrm{2}} +\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }\:=\boldsymbol{\mathrm{AB}}^{\mathrm{2}} +\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\:\:\boldsymbol{\mathrm{AB}}=\frac{\boldsymbol{\mathrm{R}}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{AC}}=\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}} \\ $$$$\:\boldsymbol{\mathrm{Pink}}\:\boldsymbol{\mathrm{Area}}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\boldsymbol{\mathrm{AB}}×\boldsymbol{\mathrm{AC}}\right)=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$$$ \\ $$$$ \\ $$$$\frac{\boldsymbol{\mathrm{Pink}}\:}{\boldsymbol{\mathrm{Blue}}}=\frac{\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}}{\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} }{\mathrm{16}}}=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}×\frac{\mathrm{16}}{\boldsymbol{\mathrm{R}}^{\mathrm{2}} }\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{X} \\ $$$$\left({Voir}\:{Resultat}\:{exact}\:\:{dessous}:\:\mathrm{3},\mathrm{1334}\right) \\ $$$$\:\: \\ $$

Commented by a.lgnaoui last updated on 28/Nov/23

Commented by mr W last updated on 28/Nov/23

wrong! BD=DF≠(R/2)

$${wrong}! \\ $$$${BD}={DF}\neq\frac{{R}}{\mathrm{2}} \\ $$

Commented by a.lgnaoui last updated on 28/Nov/23

OM=ON=R

$$\mathrm{OM}=\mathrm{ON}=\mathrm{R} \\ $$

Commented by mr W last updated on 29/Nov/23

the side length of the square is not equal to the radius of smaller semi circles!

$${the}\:{side}\:{length}\:{of}\:{the}\:{square}\:{is}\:{not} \\ $$$${equal}\:{to}\:{the}\:{radius}\:{of}\:{smaller}\:{semi} \\ $$$${circles}! \\ $$

Commented by a.lgnaoui last updated on 29/Nov/23

soit 𝛂=∡CHO tan 𝛂=((x/2)/x)=(1/2) ⇒ ((OC)/(OH))=(1/2)=((R/2)/(x+CDcos 𝛂)) 1=(R/(x+(R/2)cos 26,56)) 𝛂= (tan^(−1) (1/2))=26,56 donc ((2R)/(2x+Rcos 26,56))=1 2x+Rcos cos 26,56=2R x=((R(2−cos 26,56))/2) alors Blue Area=(1/2)(BD×x) =(x^2 /4)= ((R^2 (2−cos 26,56)^2 )/(16)) OH=x+(R/2)cos 26,56=R BC=OE=R Pink Aeea=((R^2 (√3))/8) ⇒ ((Pink Ara)/(Blue Area))=((R^2 (√3))/8)×((16)/(R^2 (2−cos 26,56))) =((2(√3))/(2−0,894466))= 3,1334

$$\mathrm{soit}\:\:\boldsymbol{\alpha}=\measuredangle\mathrm{CHO}\:\:\:\:\mathrm{tan}\:\boldsymbol{\alpha}=\frac{\boldsymbol{\mathrm{x}}/\mathrm{2}}{\boldsymbol{\mathrm{x}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{OC}}{\mathrm{OH}}=\frac{\mathrm{1}}{\mathrm{2}}=\frac{\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}}}{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{CD}}\mathrm{cos}\:\boldsymbol{\alpha}} \\ $$$$\:\mathrm{1}=\frac{\boldsymbol{\mathrm{R}}}{\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}}\mathrm{cos}\:\mathrm{26},\mathrm{56}}\:\:\boldsymbol{\alpha}=\:\left(\mathrm{tan}\:^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{26},\mathrm{56} \\ $$$$\mathrm{donc}\:\:\frac{\mathrm{2}\boldsymbol{\mathrm{R}}}{\mathrm{2}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{R}}\mathrm{cos}\:\mathrm{26},\mathrm{56}}=\mathrm{1} \\ $$$$\:\:\:\mathrm{2}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{R}}\mathrm{cos}\:\mathrm{cos}\:\mathrm{26},\mathrm{56}=\mathrm{2}\boldsymbol{\mathrm{R}} \\ $$$$\:\:\boldsymbol{\mathrm{x}}=\frac{\boldsymbol{\mathrm{R}}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{26},\mathrm{56}\right)}{\mathrm{2}} \\ $$$$\mathrm{alors}\:\:\boldsymbol{\mathrm{Blue}}\:\boldsymbol{\mathrm{Area}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\boldsymbol{\mathrm{BD}}×\boldsymbol{\mathrm{x}}\right) \\ $$$$\:\:\:=\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{4}}=\:\:\:\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{cos}\:\mathrm{26},\mathrm{56}\right)^{\mathrm{2}} }{\mathrm{16}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{OH}}=\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\mathrm{R}}}{\mathrm{2}}\mathrm{cos}\:\mathrm{26},\mathrm{56}=\boldsymbol{\mathrm{R}} \\ $$$$\boldsymbol{\mathrm{BC}}=\boldsymbol{\mathrm{OE}}=\boldsymbol{\mathrm{R}} \\ $$$$\boldsymbol{\mathrm{Pink}}\:\boldsymbol{\mathrm{Aeea}}=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$$$ \\ $$$$\Rightarrow\:\:\frac{\boldsymbol{\mathrm{Pink}}\:\boldsymbol{\mathrm{Ara}}}{\boldsymbol{\mathrm{Blue}}\:\boldsymbol{\mathrm{Area}}}=\frac{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{8}}×\frac{\mathrm{16}}{\boldsymbol{\mathrm{R}}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{cos}\:\mathrm{26},\mathrm{56}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}−\mathrm{0},\mathrm{894466}}=\:\:\:\:\mathrm{3},\mathrm{1334} \\ $$

Commented by mr W last updated on 29/Nov/23

i have said: you assumed that DB=CO. but this is wrong!!! that means tan ∠CHO ≠(1/2). therefore the rest is wrong.

$${i}\:{have}\:{said}:\:{you}\:\boldsymbol{{assumed}}\: \\ $$$${that}\:{DB}={CO}.\:{but}\:{this}\:{is}\:{wrong}!!! \\ $$$${that}\:{means}\:\mathrm{tan}\:\angle{CHO}\:\neq\frac{\mathrm{1}}{\mathrm{2}}. \\ $$$${therefore}\:{the}\:{rest}\:{is}\:{wrong}. \\ $$

Answered by mr W last updated on 29/Nov/23

Commented by mr W last updated on 29/Nov/23

r=radius of smaller semi−circles a=side length of square OA=(a/2) AD^2 =h_2 ^2 =OA×CA=(a/2)(2r−(a/2))=ar−(a^2 /4) AE^2 =h_1 ^2 =CA×AH=(2r−(a/2))(2r+(a/2))=4r^2 −(a^2 /4) ED=h_1 −h_2 =a (√(4r^2 −(a^2 /4)))−(√(ar−(a^2 /4)))=a (√(4r^2 −(a^2 /4)))−a=(√(ar−(a^2 /4))) 4r^2 −(a^2 /4)+a^2 −2a(√(4r^2 −(a^2 /4)))=ar−(a^2 /4) a^2 −ar+4r^2 =2a(√(4r^2 −(a^2 /4))) 2a^4 −2ra^3 −7r^2 a^2 −8r^3 a+16r^4 =0 let λ=(a/r) ⇒2λ^4 −2λ^3 −7λ^2 −8λ+16=0 ⇒λ≈1.0499 1335 8904 that means a≈1.049913358904r ≠r

$${r}={radius}\:{of}\:{smaller}\:{semi}−{circles}\: \\ $$$${a}={side}\:{length}\:{of}\:{square} \\ $$$${OA}=\frac{{a}}{\mathrm{2}} \\ $$$${AD}^{\mathrm{2}} ={h}_{\mathrm{2}} ^{\mathrm{2}} ={OA}×{CA}=\frac{{a}}{\mathrm{2}}\left(\mathrm{2}{r}−\frac{{a}}{\mathrm{2}}\right)={ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${AE}^{\mathrm{2}} ={h}_{\mathrm{1}} ^{\mathrm{2}} ={CA}×{AH}=\left(\mathrm{2}{r}−\frac{{a}}{\mathrm{2}}\right)\left(\mathrm{2}{r}+\frac{{a}}{\mathrm{2}}\right)=\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${ED}={h}_{\mathrm{1}} −{h}_{\mathrm{2}} ={a} \\ $$$$\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}−\sqrt{{ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}={a} \\ $$$$\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}−{a}=\sqrt{{ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{a}^{\mathrm{2}} −\mathrm{2}{a}\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}={ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${a}^{\mathrm{2}} −{ar}+\mathrm{4}{r}^{\mathrm{2}} =\mathrm{2}{a}\sqrt{\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} −\mathrm{2}{ra}^{\mathrm{3}} −\mathrm{7}{r}^{\mathrm{2}} {a}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{3}} {a}+\mathrm{16}{r}^{\mathrm{4}} =\mathrm{0} \\ $$$${let}\:\lambda=\frac{{a}}{{r}} \\ $$$$\Rightarrow\mathrm{2}\lambda^{\mathrm{4}} −\mathrm{2}\lambda^{\mathrm{3}} −\mathrm{7}\lambda^{\mathrm{2}} −\mathrm{8}\lambda+\mathrm{16}=\mathrm{0} \\ $$$$\Rightarrow\lambda\approx\mathrm{1}.\mathrm{0499}\:\mathrm{1335}\:\mathrm{8904} \\ $$$${that}\:{means}\:{a}\approx\mathrm{1}.\mathrm{049913358904}{r}\:\neq{r} \\ $$

Commented by mr W last updated on 29/Nov/23

((EG)/(ED))=((AB)/(AD))=((r−(a/2))/( (√(ar−(a^2 /4)))))=((2−λ)/( (√(4λ−λ^2 )))) blue area=((ED×EG)/2)=((λ^2 (2−λ)r^2 )/( 2(√(4λ−λ^2 )))) FE^2 +FB^2 =BA^2 +AE^2 FE^2 +r^2 =(r−(a/2))^2 +(4r^2 −(a^2 /4)) FE^2 =4r^2 −ar FE=r(√(4−λ)) pink area =((FB×FE)/2)=((r^2 (√(4−λ)))/2) ((pink)/(blue))=((√(4−λ))/2)×((2(√(4λ−λ^2 )))/(λ^2 (2−λ))) =((4−λ)/((2−λ)λ(√λ)))≈2.886299319

$$\frac{{EG}}{{ED}}=\frac{{AB}}{{AD}}=\frac{{r}−\frac{{a}}{\mathrm{2}}}{\:\sqrt{{ar}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}}=\frac{\mathrm{2}−\lambda}{\:\sqrt{\mathrm{4}\lambda−\lambda^{\mathrm{2}} }} \\ $$$${blue}\:{area}=\frac{{ED}×{EG}}{\mathrm{2}}=\frac{\lambda^{\mathrm{2}} \left(\mathrm{2}−\lambda\right){r}^{\mathrm{2}} }{\:\mathrm{2}\sqrt{\mathrm{4}\lambda−\lambda^{\mathrm{2}} }} \\ $$$${FE}^{\mathrm{2}} +{FB}^{\mathrm{2}} ={BA}^{\mathrm{2}} +{AE}^{\mathrm{2}} \\ $$$${FE}^{\mathrm{2}} +{r}^{\mathrm{2}} =\left({r}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{4}{r}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${FE}^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} −{ar} \\ $$$${FE}={r}\sqrt{\mathrm{4}−\lambda} \\ $$$${pink}\:{area}\:=\frac{{FB}×{FE}}{\mathrm{2}}=\frac{{r}^{\mathrm{2}} \sqrt{\mathrm{4}−\lambda}}{\mathrm{2}} \\ $$$$\frac{{pink}}{{blue}}=\frac{\sqrt{\mathrm{4}−\lambda}}{\mathrm{2}}×\frac{\mathrm{2}\sqrt{\mathrm{4}\lambda−\lambda^{\mathrm{2}} }}{\lambda^{\mathrm{2}} \left(\mathrm{2}−\lambda\right)} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4}−\lambda}{\left(\mathrm{2}−\lambda\right)\lambda\sqrt{\lambda}}\approx\mathrm{2}.\mathrm{886299319} \\ $$

Commented by mr W last updated on 29/Nov/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com