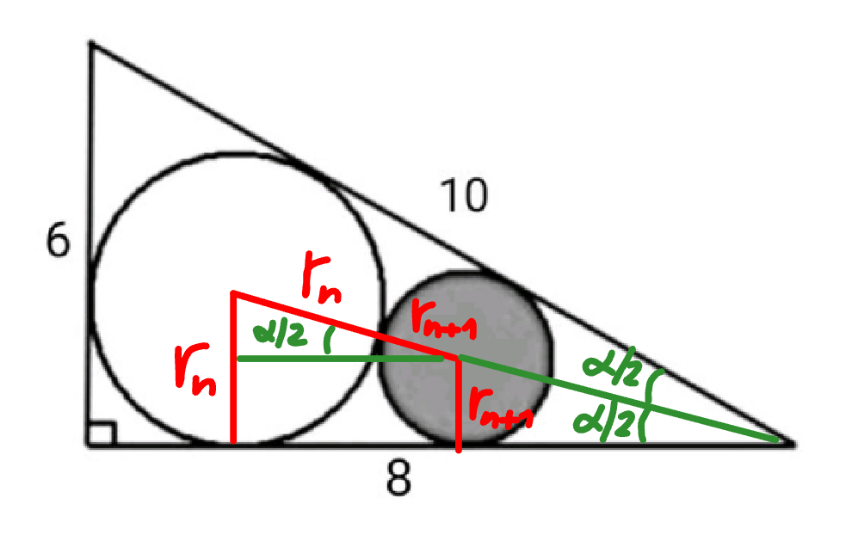
Question Number 201008 by Mingma last updated on 27/Nov/23
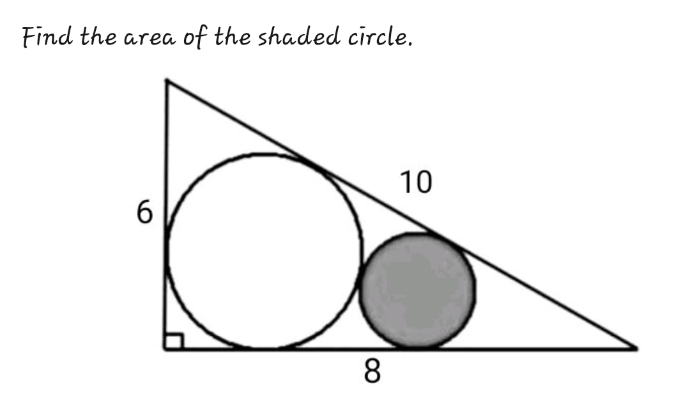
Answered by mr W last updated on 28/Nov/23
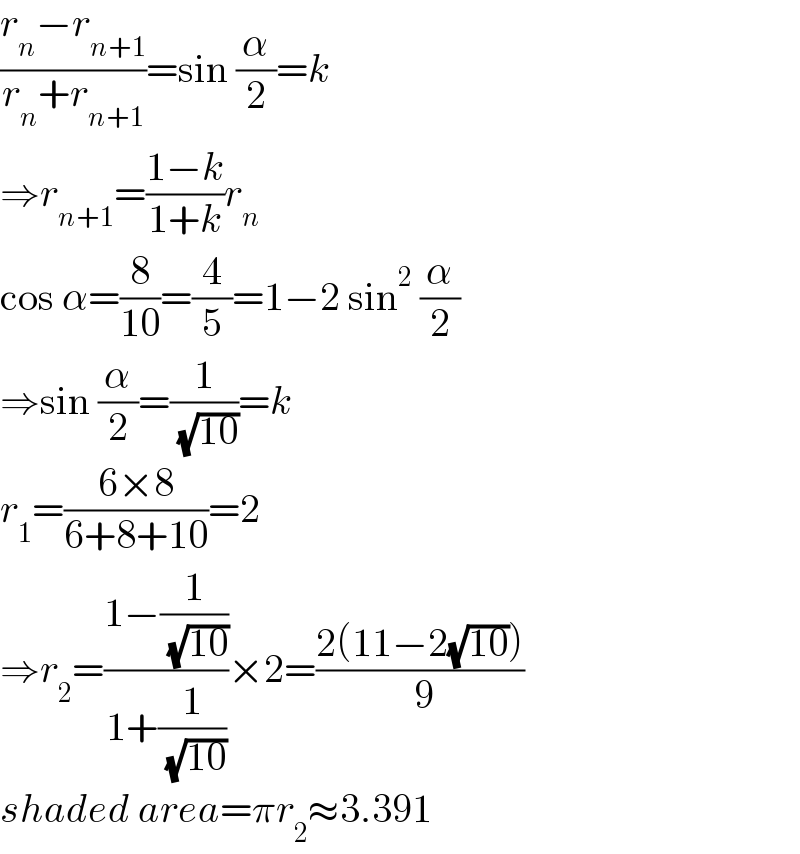
$$\frac{{r}_{{n}} −{r}_{{n}+\mathrm{1}} }{{r}_{{n}} +{r}_{{n}+\mathrm{1}} }=\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}={k} \\ $$$$\Rightarrow{r}_{{n}+\mathrm{1}} =\frac{\mathrm{1}−{k}}{\mathrm{1}+{k}}{r}_{{n}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{8}}{\mathrm{10}}=\frac{\mathrm{4}}{\mathrm{5}}=\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}={k} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{6}×\mathrm{8}}{\mathrm{6}+\mathrm{8}+\mathrm{10}}=\mathrm{2} \\ $$$$\Rightarrow{r}_{\mathrm{2}} =\frac{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}}{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}}×\mathrm{2}=\frac{\mathrm{2}\left(\mathrm{11}−\mathrm{2}\sqrt{\mathrm{10}}\right)}{\:\mathrm{9}} \\ $$$${shaded}\:{area}=\pi{r}_{\mathrm{2}} \approx\mathrm{3}.\mathrm{391} \\ $$
Commented by Mingma last updated on 28/Nov/23
Nice solution, sir!
Commented by Mingma last updated on 28/Nov/23
Can you show your diagram of explanation?
Commented by mr W last updated on 28/Nov/23